Etykietowanie (numerowanie) ciągu¶
$S = (s_1, s_2, \cdots, s_t)$ - ciąg ze zbioru o maksymalnie $n$ elementach ($t \leq n$)
$X[1], X[2], \cdots X[t]$ - etykietowanie (numerowanie) ciągu:
- $s_i = s_j \Leftrightarrow X[i] = X[j]$, dla $1 \leq i,j \leq t$ (spójność etykietowania),
- $X[i] \in [1..n]$ dla $1 \leq i \leq t$ (zbiór etykiet),
- $X[i]$ jest pozycją (rangą) elementu $s_i$ w uporządkowanej liście zawierającej wszystkie, różne wartości występujące w $S$ (etykietowanie uporządkowane).
$k$-ekwiwalecja¶
Mówimy, że w tekście o długości $n$ dwie pozycje są $k$-ekwiwalentne, gdy składowe o długości $k$ zaczynające się na tych pozycjach są sobie równe.
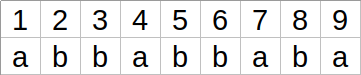
Przykładowe $k$-ekwiwalentne pozycje:
Pozycje 1 i 4 są 5-ekwiwalentne.¶
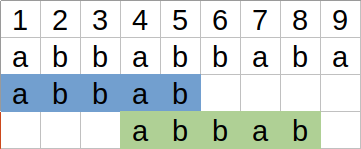
Pozycje 2 i 5 są 4-ekwiwalentne.¶
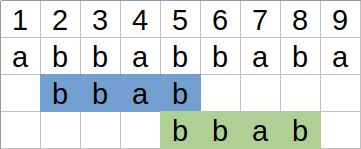
Pozycje 3 i 6 są 3-ekwiwalentne.¶
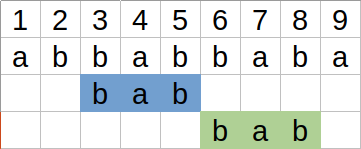
Tablica etykiet¶
$k$-ekwiwalencję oznacza się poprzez wprowadzenie etykietowania, które przy ustalonym $k$ daje te same etykiety pozycjom ekwiwalentnym. Wymaga się, aby to etykietowanie było uporządkowane. Tablicę etykiet oznacza się przez $Name_k$, a składowa na pozycji $i$ oznaczana jest jako $Name_k[i]$.

Wymagam zatem np. żeby $Name_4[1] = Name_4[4]$.
Nazwą (etykietą) podciągu o długości $k$ jest jego pozycja w tablicy $Name_k$.

Przyjmując $k=4$ dla powyższego ciągu mamy:
2 7 5 2 7 4 1 6 3dla następujących składowych (etykietowanie uporządkowe wg kolejności alfabetycznej):
a b a #a b b aa # # #b a b ab a b bb a # #b b a b
Uwaga: # dodaje się na końcu tekstu (przyjmując, że w porządku liter znak ten występuje po wszystkich innych literach), po to by składowe na końcu tekstu były zdefiniowane.
Tablica odesłań¶
Poza tablicą $Name_k$ definiuje się również tablicę odesłań oznaczaną $Pos_k$, która dla każdej unikalnej składowej zawiera odesłania do przykładowego jej wystąpienia w tekście.
Przykładowo dla tekstu
1 2 3 4 5 6 7 8 9
a b b a b b a b a # # #Mamy następujące odesłania (przyjęto pierwsze wystąpienie w tekście):
a b a #$\rightarrow$ 7a b b a$\rightarrow$ 1a # # #$\rightarrow$ 9b a b a$\rightarrow$ 6b a b b$\rightarrow$ 3b a # #$\rightarrow$ 8b b a b$\rightarrow$ 2
Słownik podstawowych składowych¶
Tablice $Name$ oraz $Pos$ dla wartości $k$ będących potęgami liczby 2 niewiększymi od długości danego tekstu $w$ nazywamy słownikiem podstwowych składowych i oznaczamy DBF(w) (dictionary of basic factors).
Wyszukiwanie w oparciu o DBF¶
Korzystając z tablicy $Name_k$, gdzie $k$ to długość wzroca (przyjmijmy w tej chwili, że $k$ jest potęgą dwójki), tworzymy ciąg:
pattern&text
gdzie & to znak spoza alfabetu. Tworzymy tablicę $Name_k$ i odczytujemy z niej wartość $Name_k[1] = q$.
Wzorzec pattern występuje na wszystkich pozycjach $i$ w tekście text, takich że $Name_k[i+k+1] = q$.
Przykład¶
Dla wzorca bb oraz tekstu abbabbaba:
1 2 3 4 5 6 7 8 9 10 11 12
b b & a b b a b b a b a # # #mamy:
6 4 1 2 6 5 2 6 5 2 5 3Zatem wzorzec bb, który ma etykietę $6$, występuje na pozycjach $5 - 2 - 1 = 2$ oraz $8 - 3 = 5$.
sort-rename¶
Funkcja sort-rename służy do wyliczenia uporządkowanego etykietowania dla ciągu $S$.
Przyjmując ciąg $S$:
(1,2), (3,1), (2,2), (1,1), (2,3), (1,2)
W pierwszym korku dodajemy do elemetu indeks jego wystąpienia:
((1,2),1), ((3,1),2), ((2,2),3), ((1,1),4), ((2,3),5), ((1,2),6)
Następnie sortujemy leksykograficznie elemety tego ciągu:
((1, 1), 4), ((1, 2), 1), ((1, 2), 6), ((2, 2), 3), ((2, 3), 5), ((3, 1), 2)
W kolejnym kroku klastrujemy elementy o tej samej wartości pierwszej składowej:
((1, 1), [4]), ((1, 2), [1,6]), ((2, 2), [3]), ((2, 3), [5]), ((3, 1), [2])
Otrzymujemy etykiety:
(1, 1), [4](1, 2), [1,6](2, 2), [3](2, 3), [5](3, 1), [2]
Dla wejściowego ciągu:
(1,2), (3,1), (2,2), (1,1), (2,3), (1,2)
otrzymujemy tablicę $Name$:
(2, 5, 3, 1, 4, 2)
oraz $Pos$:
(4, 1, 3, 5, 2)
def sort_rename(sequence):
last_value = None
last_index = None
cluster_index = 0
name = [None] * len(sequence)
pos = {}
# dodajemy indeks oraz sortujemy elementy
for value, index in sorted([(e,i) for i,e in enumerate(sequence)]):
# klastrujemy elementy
if(last_value and last_value != value):
cluster_index += 1
pos[cluster_index] = index
# uzupełniamy tablicę nazw
name[index] = cluster_index
if last_value is None:
pos[0] = index
last_value, last_index = value, index
return (name, pos)
sort_rename([(1,2), (3,1), (2,2), (1,1), (2,3), (1,2)])
([1, 4, 2, 0, 3, 1], {0: 3, 1: 0, 2: 2, 3: 4, 4: 1})
from random import randint
size = 10
max_value = 5
a = [randint(0,max_value-1) for i in range(size)]
print(a)
count = [0 for i in range(max_value)]
for i in a:
count[i] += 1
print(count)
total = 0
for v in range(max_value):
count[v], total = total, count[v] + total
print(count)
indices = []
for i in a:
indices.append(count[i])
count[i] += 1
print(indices)
result = [0 for i in range(size)]
for i in range(len(a)):
result[indices[i]] = a[i]
print(result)
[0, 3, 2, 3, 3, 3, 0, 0, 1, 1] [3, 2, 1, 4, 0] [0, 3, 5, 6, 10] [0, 6, 5, 7, 8, 9, 1, 2, 3, 4] [0, 0, 0, 1, 1, 2, 3, 3, 3, 3]
Algorytm KMR¶
Działanie algorytmu opiera się na prostym fakcie:
$Name_{2k} = sort-rename(composite-name_k)$
Gdzie, $composite-name_k$ definiowany jest jako:
$composite-name_k[i] = (Name_k[i], Name_k[i+k])$
import math
def kmr(text):
original_length = len(text)
factor = math.floor(math.log2(len(text)))
max_lenght = 2 ** factor
padding_lenght = 2 ** (factor + 1) - 1 - original_length
text += "z" * padding_lenght
name, pos = sort_rename(list(text))
names = {1: name}
entries = {1: pos}
for i in range(1, factor):
power = 2 ** (i - 1)
new_sequence = []
for j in range(len(text)):
if(j+power < len(names[power])):
new_sequence.append((names[power][j], names[power][j+power]))
name, pos = sort_rename(new_sequence)
names[power * 2] = name
entries[power * 2] = pos
return (names, entries)
text = "abaabbaa"
names, entries = kmr(text)
print("names:")
for k,v in names.items():
print(k, [e+1 for e in v[:len(text)]])
print("\npositions:")
for k,v in entries.items():
print(k, [v[e]+1 for e in range(len(v)-1)])
strings = [text[v[e]:v[e]+k] for e in range(len(v) -1)]
print(" ", [ s + "z" * (k-len(s)) for s in strings] )
names: 1 [1, 2, 1, 1, 2, 2, 1, 1] 2 [2, 4, 1, 2, 5, 4, 1, 3] 4 [3, 6, 1, 4, 8, 7, 2, 5] positions: 1 [1, 2] ['a', 'b'] 2 [3, 1, 8, 2, 5] ['aa', 'ab', 'az', 'ba', 'bb'] 4 [3, 7, 1, 4, 8, 2, 6, 5] ['aabb', 'aazz', 'abaa', 'abba', 'azzz', 'baab', 'baaz', 'bbaa']
Złożoność obliczeniowa KMR¶
Jeśli skorzystamy z sortowania przez zliczanie to otrzymamy złożoność $O(n * log(n))$.
Co z składowymi o długościach nie będących potęgą 2?¶
$Name_q[i] = Name_q[j] \Leftrightarrow$ $ (Name_t[i]=Name_t[j] \land Name_t[i+q-t] = Name_t[j+q-t])$,
gdzie:
$t = max\{r: r = 2 ^ i \land r < q\}$
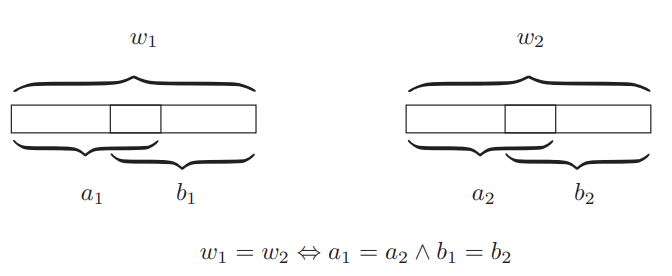
Zastosowanie¶
- poszukiwanie najdłuższej składowej występującej co najmniej 2 razy w tekście
- poszukiwanie najdłuższej składowej występującej co najmniej k-razy w tekście
Ad. 1,2¶
Liniowo przeglądamy tablicę $Name$ i zliczamy wystąpienia elementów (można to zrobić w ramach procedury klastrowania).
Ad. 2¶
Jeśli $k>2$ to procedura wygląda w ten sposób, że dla ustalonego $k$ szukamy ciągu o długości $r$, który spełnia ten warunek (w ciągu o długości $n$ łańcuch ten może mieć maksymalnie długość $n-k+1$). Wartość $r$ poszukujemy korzystając z wyszukiwania binarnego: $1 \leq r \leq n-k+1$, korzystając z faktu, że jeśli $r_1 < r_2$ i dla $r_2$ istnieje taki ciąg, to dla $r_1$ też istnieje taki ciąg.
Te same wyniki można uzyskać korzystając z drzewa sufiksów, ale algorytm sortowania składowych jest znacznie prostszy.
print(regular_pairs(50))
[(0, 49), (0, 32, 49), (0, 16, 32, 48, 49), (0, 8, 16, 24, 32, 40, 48, 49), (0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 49), (0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 49), (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49)]