Tagowanie morfosyntaktyczne¶


dr inż. Aleksander Smywiński-Pohl¶

apohllo@agh.edu.pl¶

http://apohllo.pl/dydaktyka/nlp¶

konsultacje: czw. 16:30-17:30¶

Części mowy - klasyfikacja tradycyjna¶

  • odmienne
    • rzeczownik, np. kość
    • przymiotnik, np. twarda
    • czasownik, np. gryźć
    • liczebnik, np. siedem
    • zaimek (część), np. mój
    • przysłówek, np. szybko

 

  • nieodmienne
    • zaimek (część), np. tam
    • przyimek, np. do
    • spójnik, np. i
    • wykrzyknik, np. aha
    • partykuła, np. nie

Części mowy - klasy otwarte i zamknięte¶

  • klasy otwarte: rzeczownik, czasownik, przymiotnik, przysłówek
  • klasy zamknięte: pozostałe

$\rightarrow$ powstawanie nowych wyrazów zarezerwowane jest do klas otwartych, np. iPhone, lockdown

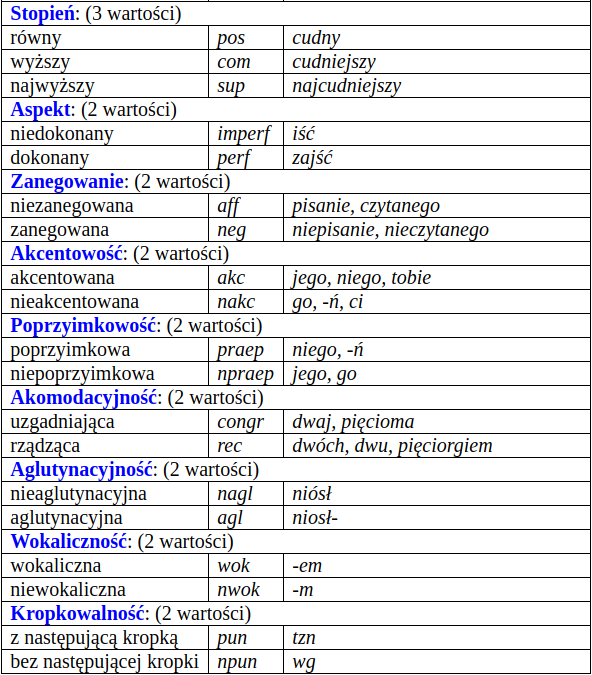
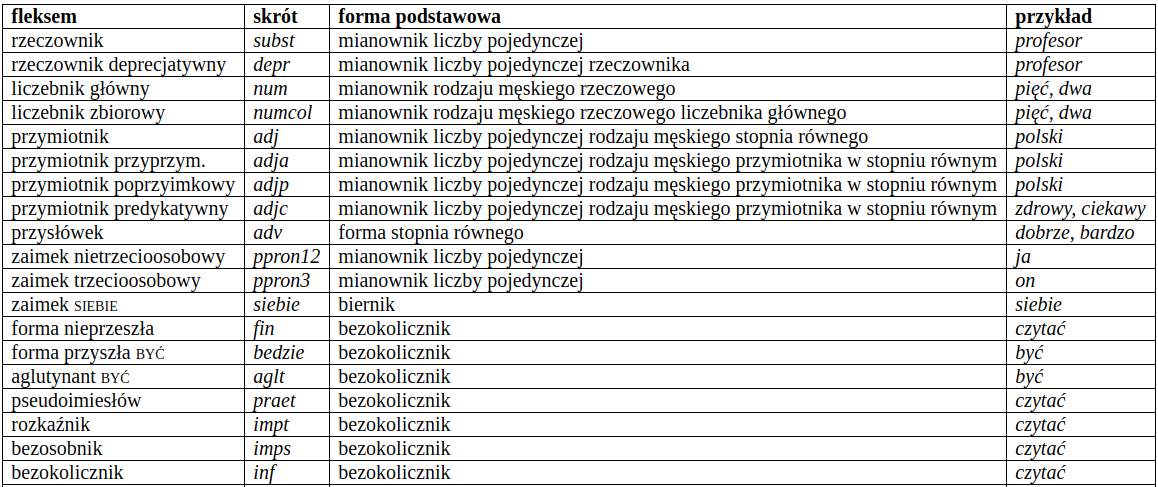
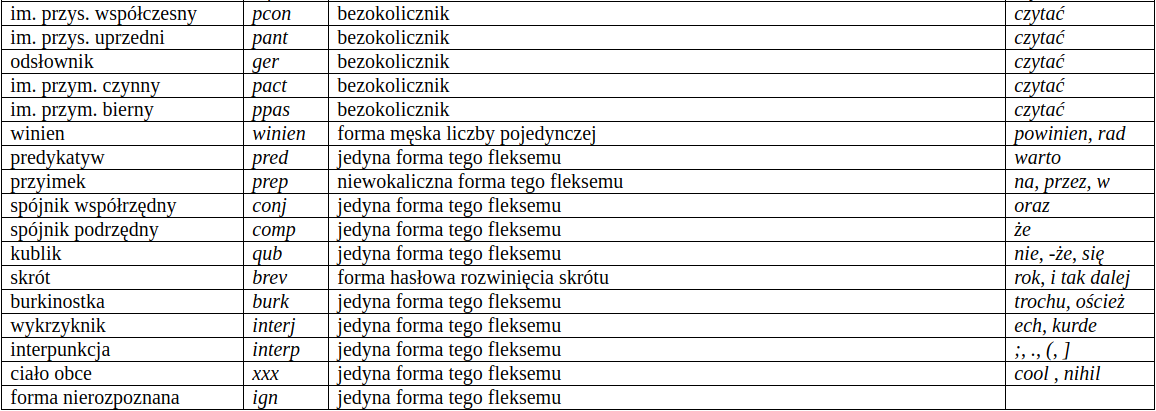
Kategorie gramatyczne 1/2 w Narodowym Korpusie Języka Polskiego (NKJP)¶

http://nkjp.pl/poliqarp/help/plse2.html

Kategorie gramatyczne 2/2¶

http://nkjp.pl/poliqarp/help/plse2.html

Klasy fleksyjne 1/2¶


http://nkjp.pl/poliqarp/help/plse2.html

Klasy fleksyjne 2/2¶


http://nkjp.pl/poliqarp/help/plse2.html

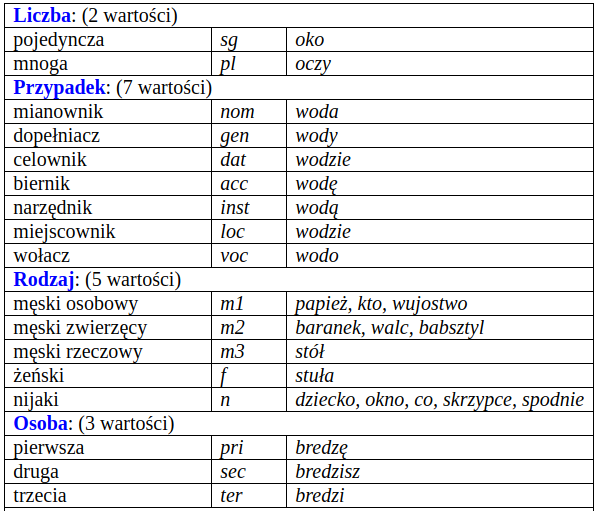
Kompatybilność kategorii i klas¶

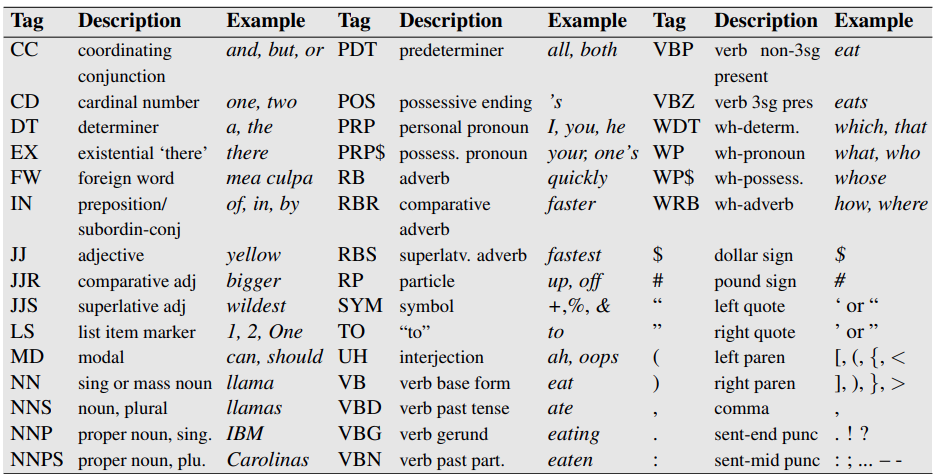
Klasy fleksyjne Universal Dependencies 2.0¶

  • ADJ: adjective, np. big
  • ADV: adverb, np. very
  • AUX: auxiliary, np. must
  • CCONJ: coordinating conjunction, np. and
  • DET: determiner, np. the
  • INTJ: interjection, np. psst
  • NOUN: noun, np. apple
  • NUM: numeral, np. one
  • PART: particle, np. not

https://universaldependencies.org/u/pos/all.html

 

  • PRON: pronoun, np. you
  • PROPN: proper noun, np. Mary
  • PUNCT: punctuation, np. !
  • SCONJ: subordinating conjunction, np. that
  • SYM: symbol, np. 😝
  • VERB: verb, np. run
  • X: other, np. xfgh

Tagi w korpusie Penn Treebank¶


Tagowanie morfosyntaktyczne¶


Partia           partia         subst:sg:nom:f
polityczna       polityczny     adj:sg:nom:f:pos
jest             być            fin:sg:ter:imperf
dobrowolną       dobrowolny     adj:sg:inst:f:pos
organizacją      organizacja    subst:sg:inst:f
,                ,              interp
występującą      występować     pact:sg:inst:f:imperf:aff
pod              pod            prep:inst:nwok
określoną        określony      adj:sg:inst:f:pos
nazwą            nazwa          subst:sg:inst:f

Jest to zadanie należące do kategorii dezambiguacji, tzn. należy wybrać jedną z dostępnych możliwości.

W opisie morfologicznym na pierwszym miejscu występuje klasa fleksyjna, a na pozostałych wartości adekatnych kategorii gramatycznych.

Liczba możliwych kombinacji wartości dla języka polskiego przekracza 1000. Dla języka angileskiego - w zależności od tagsetu - Penn Treebank 45 tagów, korpus Browna 87 tagów. Widać więc, że zadanie tagowania posiada znacząco różną trudność dla różnych języków.

Zastosowania tagowania morfosyntaktycznego¶

  • ulepszona lematyzacja
  • ilościowa analiza korpusów pod względem morfologii
  • informacja wejściowa dla wielu innych algorytmów NLP, np.
    • jednostki nazewnicze
    • parsing
    • koreferencja

Przykłady dezambiguacji¶

Lewandowski nie strzelił żadnych goli.

subst:pl:gen:m2

rzeczownik, liczba mnoga, dopełniacz, r. męski zwierzęcy

Lewandowski goli się codziennie.

fin:sg:ter:imperf

forma nieprzeszła czasownika, liczba pojedynczy, 3 osoba, aspekt niedokonany

Lewandowski i inni mężczyźni na plaży nudystów byli goli.

adj:pl:nom:m1:pos

przymiotnik, liczba mnoga, mianownik, r. męski osobowy, stopień równy

Dopiero tagger KFTT osiąga wartość 97% poprawności tagowania - zbliżoną do języka angileskiego.

Algorytmy tagowania¶

  • ukryty model Markowa (HMM)
  • model Markowa o maksymalnej entropii (MEMM)
  • warunkowe pola losowe (CRF)
  • sieci neuronowe (NN)

Łańcuchy Markowa¶

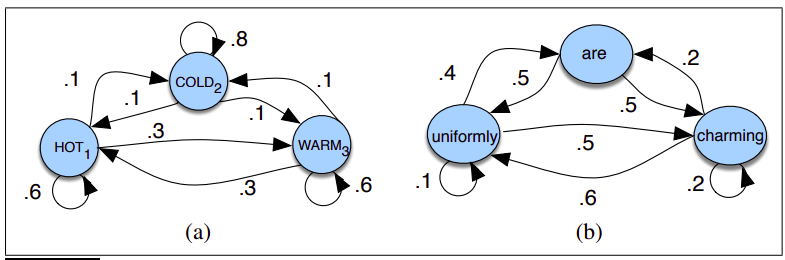
Założenie dla łańcucha Markowa 1-rzędu:

$P(q_i=a|q_1 \cdots q_{i-1}) = P(q_i=a|q_{i-1})$

Definicja łańcucha Markowa 1-rzędu¶

  • $Q = q_1, q_2, \cdots q_n$ - zbiór $N$ stanów
  • $A = q_{11}, q_{12}, q_{13}, \cdots q_{nn}$ - macierz przejścia taka, że $\sum_{j=1}^{n} a_{ij} = 1$
  • $\Pi = \pi_1, \pi_2, \cdots \pi_n$ - prawdopodobieństwo stanów początkowych, $\sum _{i=1}^{n} \pi_{i} = 1$

Ukryty model Markowa 1-rzędu (HMM)¶

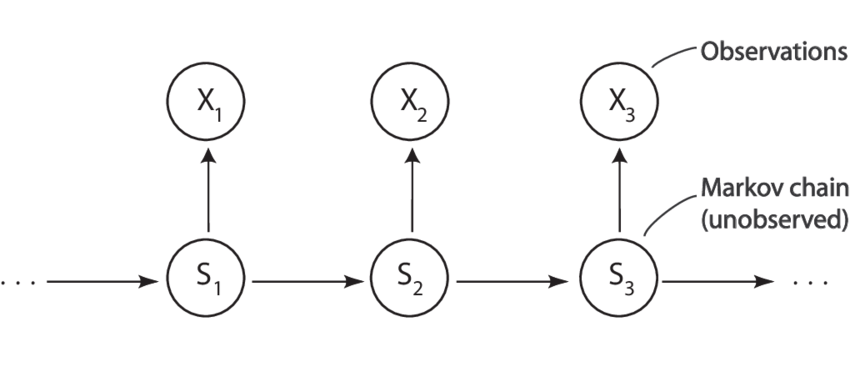
Przykład HMM¶

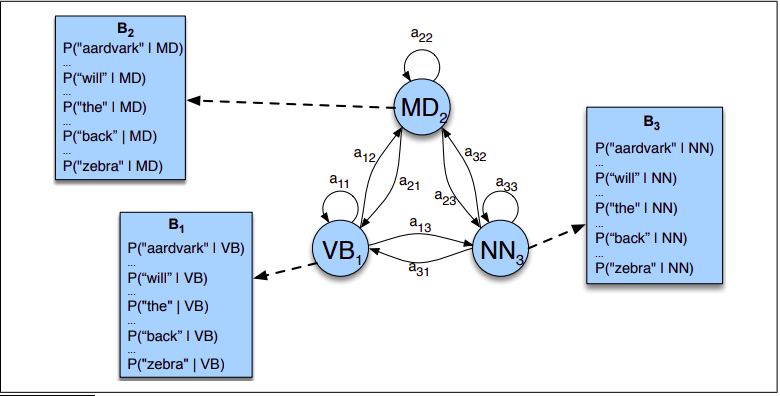
Definicja ukrytego modelu Markowa 1-rzędu¶

  • $Q = q_1, q_2, \cdots q_n$ - zbiór $N$ stanów
  • $A = q_{11}, q_{12}, q_{13}, \cdots q_{nn}$ - macierz przejścia taka, że $\sum_{j=1}^{n} a_{ij} = 1$
  • $O = o_1, o_2, o_3, \cdots, o_T$ - sekwencja $T$ obserwacji, które pochodzą ze słownika $V = v_1, v_2, \cdots, v_V$
  • $B = b_i(o_t)$ - sekwencja prawdopodobieństw obserwacji (lub emisji), wyrażających prawdopodobieństwo zaobserwowania obserwacji $o_t$ w stanie $q_i$
  • $\Pi = \pi_1, \pi_2, \cdots \pi_n$ - prawdopodobieństwo stanów początkowych, $\sum _{i=1}^{n} \pi_{i} = 1$

Założenia dla HMM¶

  • $P(q_i=a|q_1 \cdots q_{i-1}) = P(q_i=a|q_{i-1})$ - własność Markowa
  • $P(o_i| q_1, q_2, \cdots, q_T; o_1, o_2, \cdots, o_i, \cdots, o_T) = P(o_i|q_i)$ - niezależność wyjść

Tagowanie morfosyntaktyczne w oparciu o HMM¶

  • $P(t_i | t_{i-1})$ - prawdopodobieństwo wystąpienia tagu $t_i$ po tagu $t_{i-1}$
  • przykład: w szkole - subst często występuje po prep
  • $P(t_i | t_{i-1}) \cong \frac{C(t_{i-1},t_i)}{C(t_{i-1})}$
  • $P(w_i | t_i)$ - prawdopodobieństwo emisji wyrazu $w_i$ dla tegu $t_i$
  • przykład: zaimek $\rightarrow$ on - ppron3 ma duże prawdopodobieństwo "wyemitowania" zaimka "on"
  • $P(w_i | t_i) \cong \frac{C(t_i, w_i)}{C(t_i)}$

Tagowanie jako dekodowanie¶

Dekodowanie: mając na wejściu ciąg obserwacji $O = o_1, o_2, \cdots, o_T$ należy znaleźć najbardziej prawdopodobną sekwencję stanów $Q=q_1, q_2, \cdots, q_T$

$\hat t^{n}_{1} = \textrm{argmax}_{t_1^n}P(t_1^n|w_1^n)$

$\hat t^{n}_{1} = \textrm{argmax}_{t_1^n}\frac{P(w_1^n|t_1^n)P(t_1^n)}{P(w_1^n)}$

$\hat t^{n}_{1} = \textrm{argmax}_{t_1^n}P(w_1^n|t_1^n)P(t_1^n)$

$P(w_1^n|t_1^n) = \prod_{i=1}^{n}P(w_i|t_i)$

$P(t_1^n) = \prod_{i=1}^{n}P(t_i|t_{i-1})$

$\hat t^{n}_{1} = \textrm{argmax}_{t_1^n}P(t_1^n|w_1^n) \cong \textrm{argmax}_{t_1^n}\prod_{i=1}^{n}\overbrace{P(w_i|t_i)}^{\textrm{emisja}} \overbrace{P(t_i|t_{i-1})}^{\textrm{przejście}} $

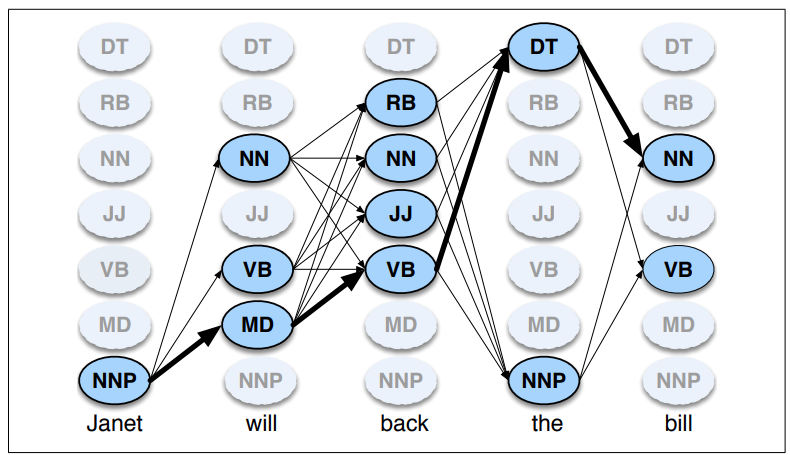
Algorytm tagowania wykorzystujący ukryty model Markowa¶

Macierz prawdopodobieństw¶

In [61]:
import numpy as np

def viterbi(observations, states, words, initial_p, transition_p, emmision_p):
    probs = np.zeros((len(observations), len(states)))
    pointers = np.zeros((len(observations), len(states)))
    word_idx = words.index(observations[0])
    for idx, state in enumerate(states):
        probs[0][idx] = initial_p[idx] * emmision_p[idx][word_idx]
        pointers[0][idx] = -1
    for o_idx, word in enumerate(observations[1:], 1):
        word_idx = words.index(observations[o_idx])
        for c_idx, c_state in enumerate(states):
            max_value, max_idx = -1, -1
            for p_idx, p_state in enumerate(states):
                value = probs[o_idx-1][p_idx] * transition_p[p_idx][c_idx]
                if(value > max_value):
                    max_value = value
                    max_idx = p_idx
            probs[o_idx][c_idx] = max_value * emmision_p[c_idx][word_idx]
            pointers[o_idx][c_idx] = max_idx
    max_value = max(probs[-1])
    
    path = []
    for idx, word in reversed(list(enumerate(observations))):
        path.insert(0, states[probs[idx].argmax(0)])
    return path, max_value
In [62]:
sequence = ["a", "dog", "barks"]
states = ["NN", "DT", "VB"]
initial_p = [0.2, 0.6, 0.2]
transition_p = [
    [0.3, 0.1, 0.6],   # from NN
    [0.7, 0.1, 0.2],   # from DT
    [0.4, 0.4, 0.2]    # from VB
]
emmision_p = [
    [0.1, 0.8, 0.1],   # from NN
    [0.8, 0.1, 0.1],   # from DT
    [0.1, 0.1, 0.8]    # from VB
]
viterbi(sequence, states, sequence, initial_p, transition_p, emmision_p)
Out[62]:
(['DT', 'NN', 'VB'], 0.129024)

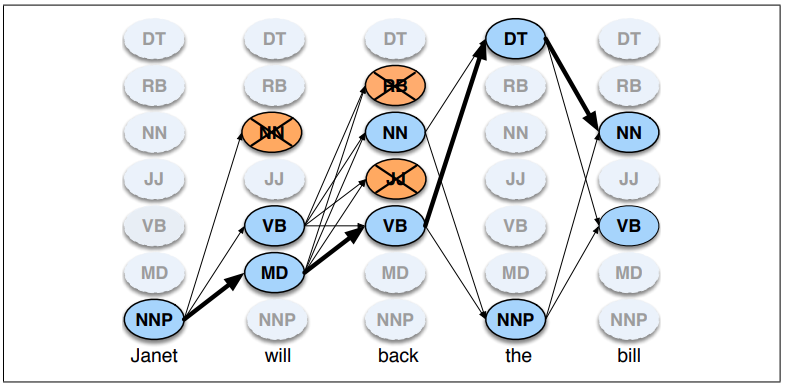
Wyszukiwanie wiązkowe (beam search)¶

Model Markowa o maksymalnej entropii (Maximum-entropy Markov Model MEMM)¶

HMM¶

$\hat t^{n}_{1} \cong \textrm{argmax}_{t_1^n}\prod_{i=1}^{n}\overbrace{P(w_i|t_i)}^{\textrm{emisja}} \overbrace{P(t_i|t_{i-1})}^{\textrm{przejście}} $

MEMM¶

$\hat t^{n}_{1} \cong \textrm{argmax}_{t_1^n}\prod_{i=1}^{n}P(t_i|w_i, t_{i-1}) $

  • MEMM może uwzględniać wiele różnych cech, o dowolnej komplikacji
  • Określenie P realizowane jest za pomocą regresji logistycznej
  • Możliwa jest realizacja dwóch przejść przez te same dane, co pozwala użyć informacji o następnym tagu, w drugim przejściu
  • dekodowanie może być zachłanne, ale znacznie lepiej sprawdza się algorytm Viterbiego!
  • istnieją jeszcze mocniejsze algorytmy, CRF i sieci neuronowe

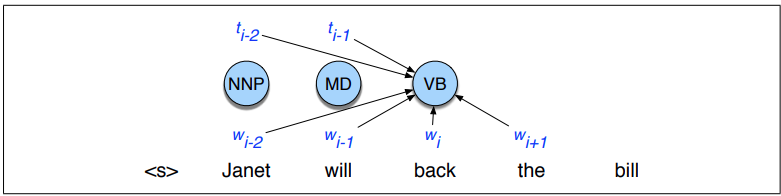
Cechy wykorzystywane przez MEMM¶

Taggery dla j. polskiego¶

  • Toygger - http://mozart.ipipan.waw.pl/~kkrasnowska/PolEval/src/
  • KRNNT - https://github.com/kwrobel-nlp/krnnt
  • COMBO - https://github.com/360er0/COMBO
  • Stanford NLP - https://stanfordnlp.github.io/stanfordnlp/installation_download.html
  • Concraft - https://github.com/kawu/concraft-pl
  • KFTT - https://github.com/kwrobel-nlp/kftt

Literatura¶

Speech and Language Processing. Daniel Jurafsky & James H. Martin, chapter 8