Podstawy sztucznej inteligencji

Temat: terminologia uczenia maszynowego

dr inż. Aleksander Smywiński-Pohl

apohllo@agh.edu.pl

https://apohllo.pl

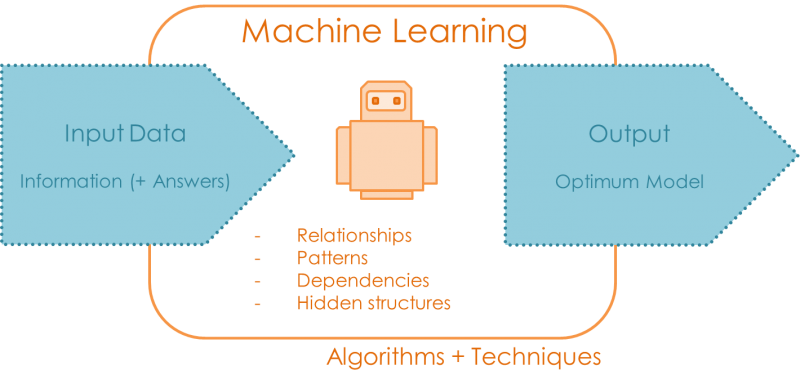
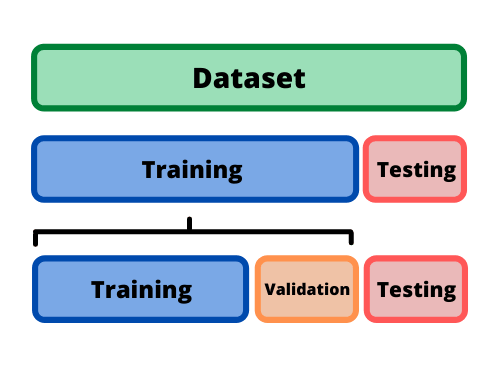
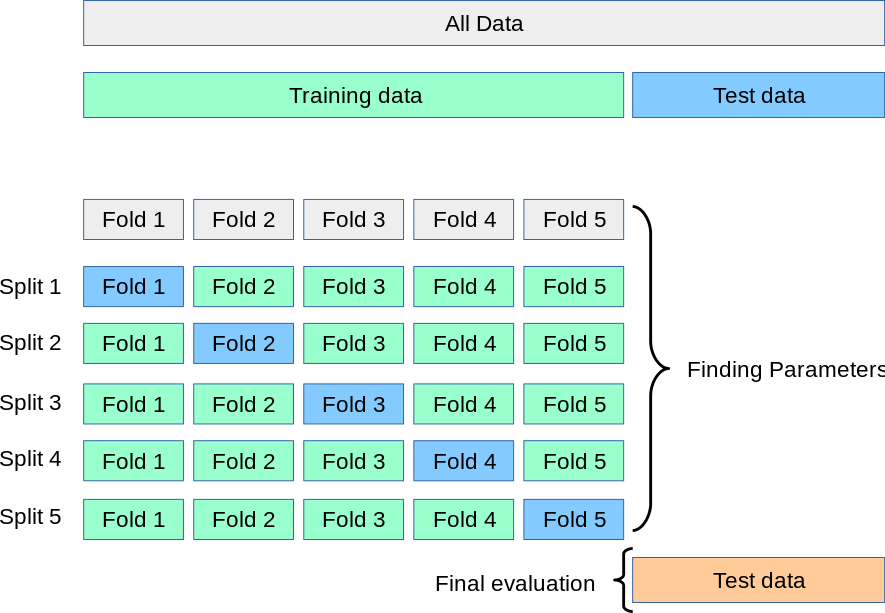
Jakie istnieją formy uczenia?

 

 

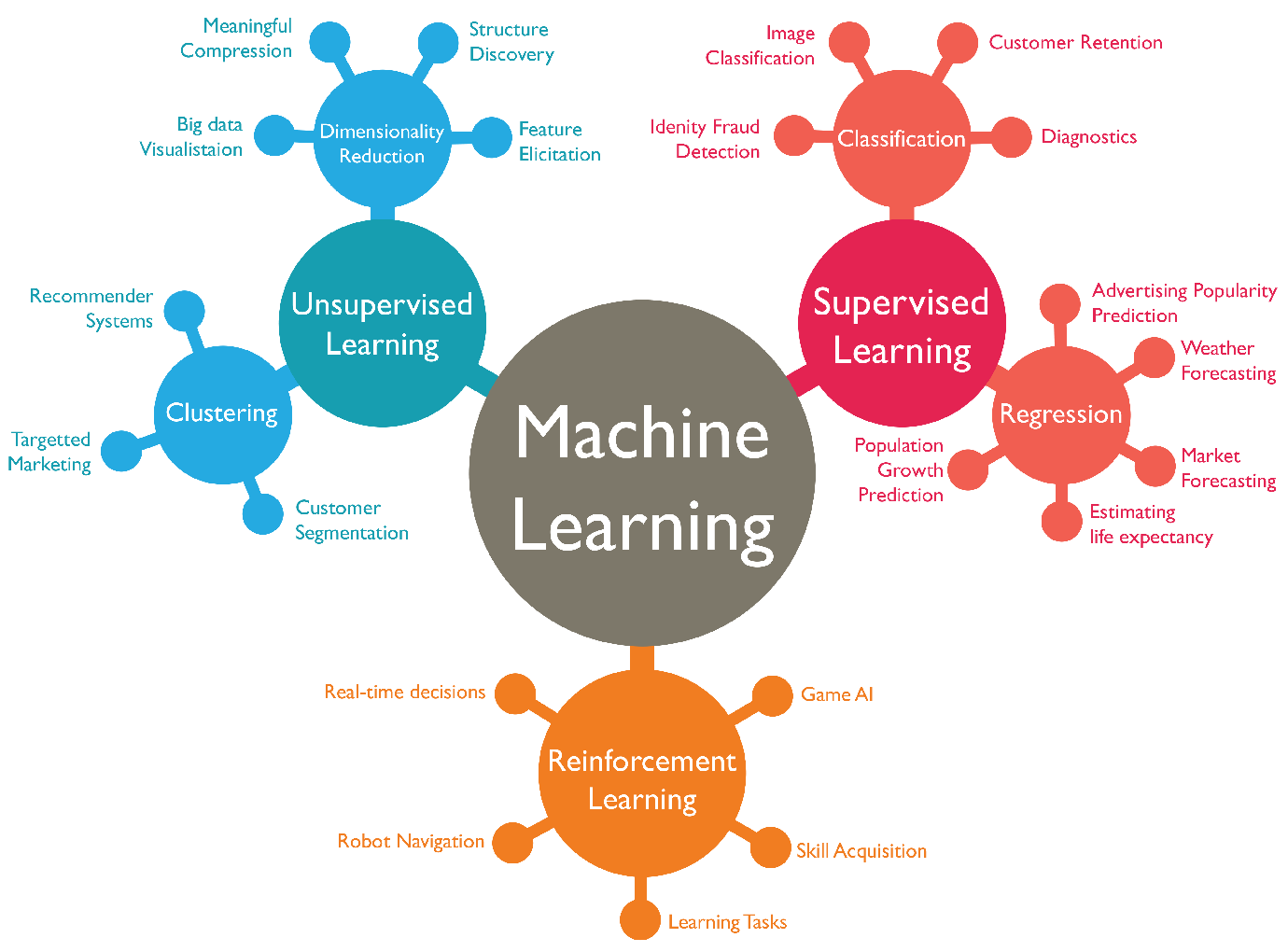
• Uczenie nadzorowane - supervised learning
• Uczenie nienadzorowane - unsupervised learning
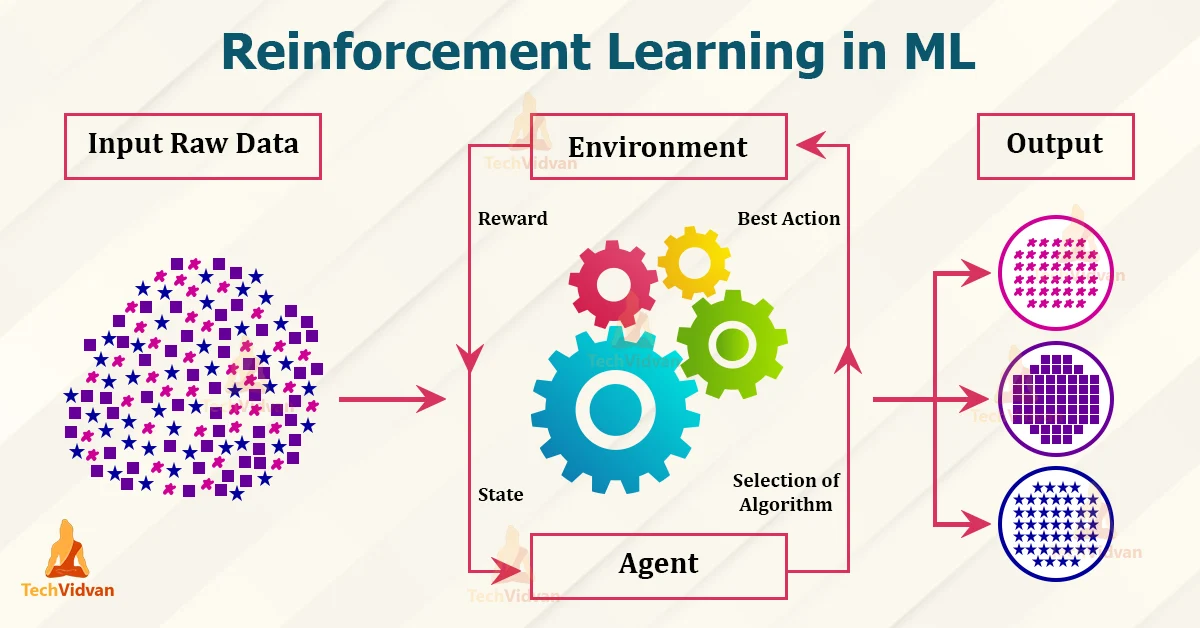
• Uczenie ze wzmocnieniem - reinforcement learning

Uczenie nadzorowane

 

 

https://quantdare.com/machine-learning-a-brief-breakdown/

• opiera się na indukcji (a nie dedukcji)
• do danych wejściowych przypisane są wartości (etykiety, liczby rzeczywiste, odpowiedzi na pytania, itp.)
• celem modelu jest znalezienie funkcji, która dla instancji danych wejściowych znajduje wartość funkcji
• kluczowym problemem jest generalizacja - zdolność do określania wartości, dla danych, które nie były widziane w trakcie uczenia

Klasyfikacja - podstawowy rodzaj uczenia nadzorowanego

 

 

https://devopedia.org/imagenet

• w klasyfikacji możemy mieć:
  • dwie klasy - klasyfikacja binarna, np. detekcja spamu
  • wiele klas - klasyfikacja wieloklasowa, np. Imagnet - 21k klas
  • wiele etykiet - klasyfikacja wieloetykietowa, etykiety przypisywane do zgłoszeń błędów na githubie
• zbiór klas jest dyskretny, skończony i najczęściej nieuporządkowany
• w klasyfikacji wieloetykietowej, wartość funkcji jest podzbiorem zbioru etykiet

Regresja - drugi podstawowy typ uczenia nadzorowanego

 

 

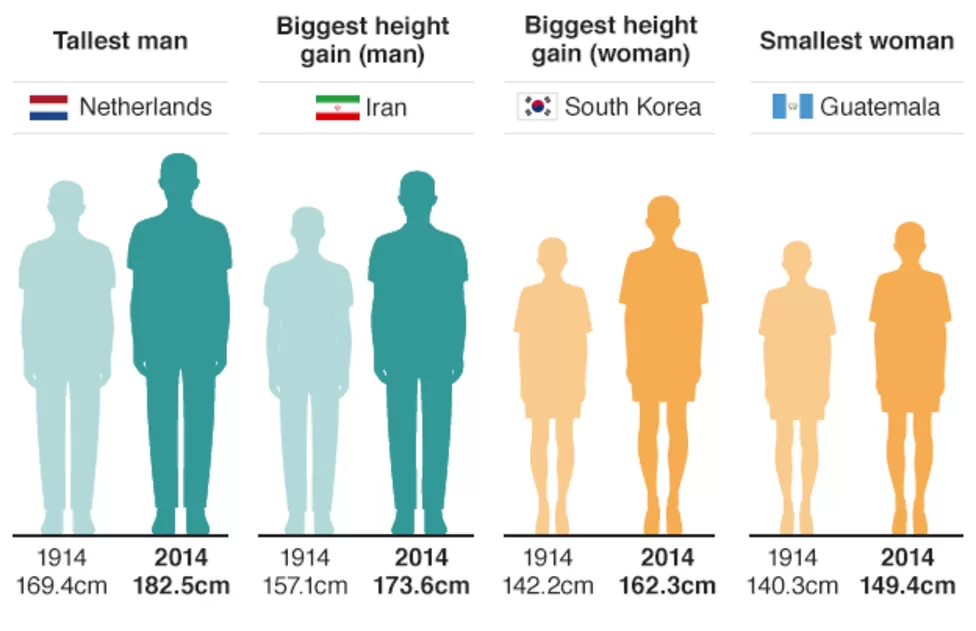
https://www.bbc.com/news/science-environment-36888541

• zbiór wartości jest najczęściej ciągły, ale może być również dyskretny (np. wiek wyrażony w latach)
• zbiór wartości jest uporządkowany
• zwykle jest to podzbiór zbioru $R^n$, bardzo często po prostu podzbiór $R$
• przykłady:
  • przewidywanie ceny na podstawie parametrów mieszkania,
  • przewidywanie oceny końcowej z pracy mgr na podstawie ocen z przedmiotów,
  • przewidywanie liczby goli w meczu na podstawie historii rozgrywek drużyn.

Dane wejściowe

• wartości liczbowe: dyskretne, ciągłe, np. temperatura, cena, liczba studentów, itp.
• wartości kategoryczne: dyskretny, skończony, nieuporządkowany zbiór wartości, np. narodowość, przedmiot na studiach, marka samochodu, płeć, itp.
• wartości binarne: szczególny typ wartości kategorycznych, objemujący tylko 2 wartości: 0 i 1, prawda/fałsz, etc.

https://huggingface.co/datasets/maharshipandya/spotify-tracks-dataset/viewer/default/train

Ocena na podstawie recenzji - regresja, czy klasyfikacja?

 

 

https://christinesunflower.com/2016/02/09/on-book-reviews-and-the-stars-rating-system/

• w niektórych przypadkach możliwe jest potraktowanie dane problemu zarówno jako problemu regresji lub problemu klasyfikacji
• dobrym przykładem jest ocena produktu przez użytkowników
• np. modele językowe lepiej radzą sobie z klasyfikacją, niż regresją

Jak można uczyć model bez nadzoru?

Uczenie nienadzorowane - klasteryzacja

 

 

https://www.kdnuggets.com/2019/09/hierarchical-clustering.html

• typowe metody uczenia nnienadzorowanego służą do znalezienia pewnego porządku w danych
• celem takiej analizy zwykle jest znalezienie pewnych wzorców, czy powiązań pomiędzy danymi, które trudno jest określić a priori, np. ze względu na brak uporządkowania danych
• celem uczenia zwykle jest redukcja złożoności danych

Modelowanie tematów - przykład redukcji wymiarowości

 

 

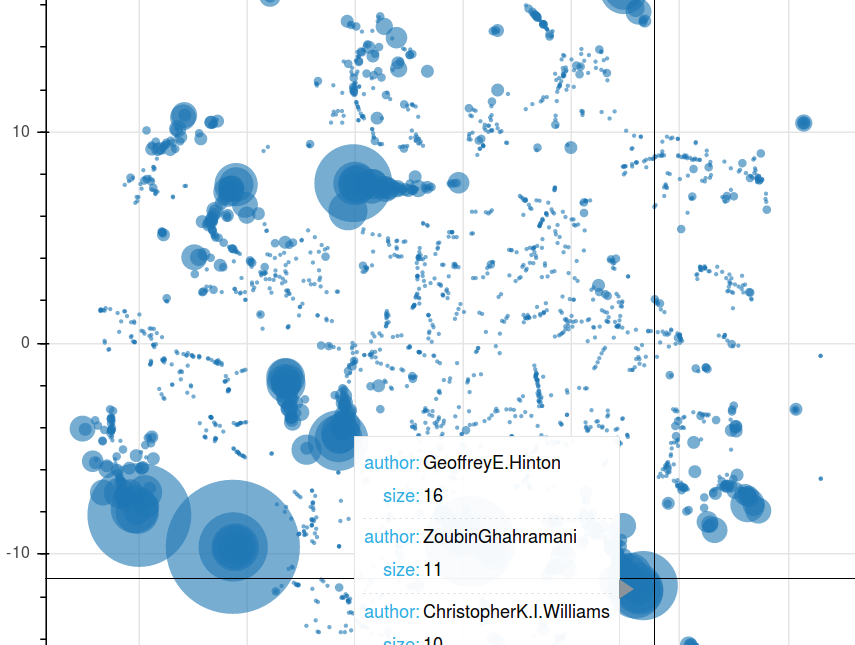
https://rare-technologies.com/new-gensim-feature-author-topic-modeling-lda-with-metadata/

• celem modelowania tematów jest przypisanie dokumentów do tematów
• temat jest definiowany przez zbiór wyrazów, dla których przypisana jest waga przynależności do tematu
• przynależność dokumentu do tematu, również określana jest wagą
• możliwe jest zwizualizowanie klastrów dokumentów poprzez projekcję do przestrzeni 2d
• redukcja odbywa się z użyciem SVD

Maskowane modelowanie języka - uczenie samonadzorowane

 

 

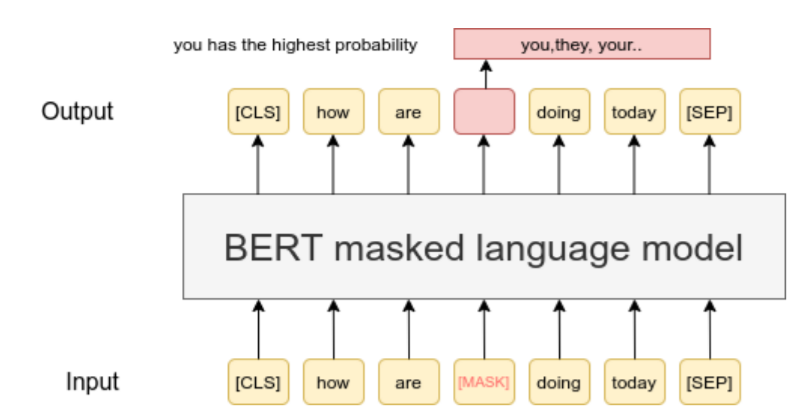
https://www.sbert.net/examples/unsupervised_learning/MLM/README.html

• Modelowanie języka (w tym wypadku maskowane) jest przykładem ciekawego typu uczenia nienadzorowanego
• Dane nie muszą być etykietowane, ale samo uczenie ma określony cel - jest nim odgadnięcie zasłoniętego słowa
• W tym przypadku brak etykiet oznacza to, że nie musiały być one "ręcznie" dodane, ponieważ wykorzystujemy po prostu duży zbiór danych tekstowych (nieoznaczonych)
• Ale struktura uczenia jest typowa dla uczenia nadzorowanego - mamy dane wejściowe oraz oczekiwane dane wyjściowe
• Obecnie często nazywa się je uczeniem samo-nadzorowanym lub uczeniem reprezentacji

Uczenie ze wzmocnieniem

 

 

https://www.sbert.net/examples/unsupervised_learning/MLM/README.html

Granie w gry - przykład RL

 

 

https://www.pcmag.com/news/7-forgotten-atari-2600-classics

ChatGPT - przykład RL

 

 

https://openai.com/research/instruction-following

Uczenie nadzorowane - definicja

Mając dany zbiór treningowy par

$$ (x_1, y_1), (x_2, y_2), (x_3, y_3), \ldots, (x_n, y_n) $$

generowanych przez funkcję $f(x)$, znaleźć funkcję $h$, która aproksymuje funkcję $f$.

Funkcja $h$ zwana jest hipotezą, a przestrzeń z której jest wybierana przestrzenią hipotez H.

Alternatywnie mówimy, że $h$ jest modelem danych, wybieranym z określonej klasy modeli H.

Dopasowanie hipotezy do danych

Oczekujemy, że funkcja $h$ będzie spójna z danymi uczącymi, tzn. najlepiej jeśli $h(x_i) = y_i$.

 

 

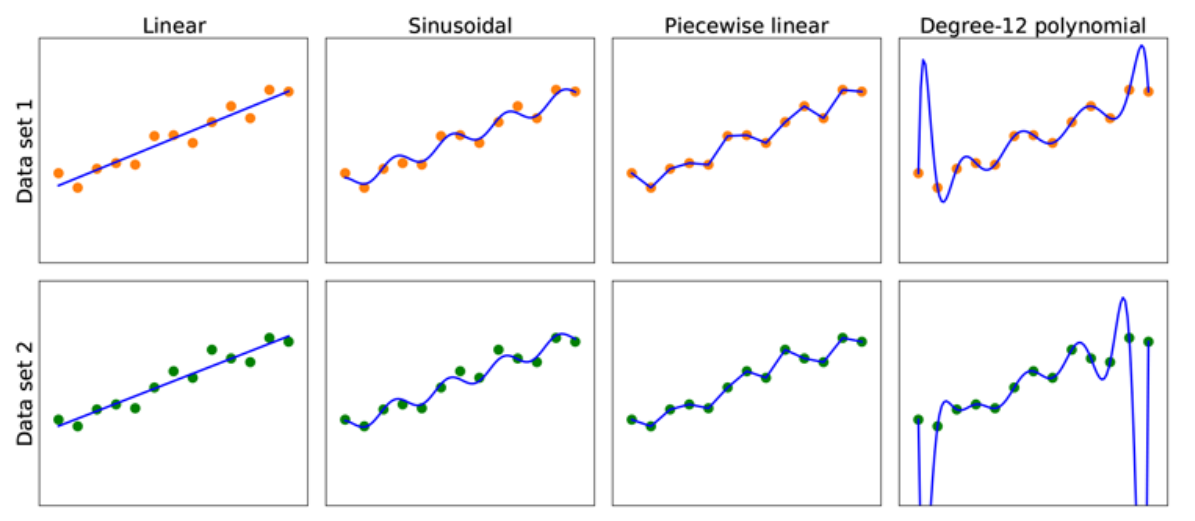
S. Russel, P. Norvig, AIMA 4rd edition

Obciążenie i wariancja

Obciążenie - tendencja hipotezy $h$ do różnienia się od oczekiwanego wyniku (wartości oczekiwanej), w przypadku treningu na różnych zbiorach danych.

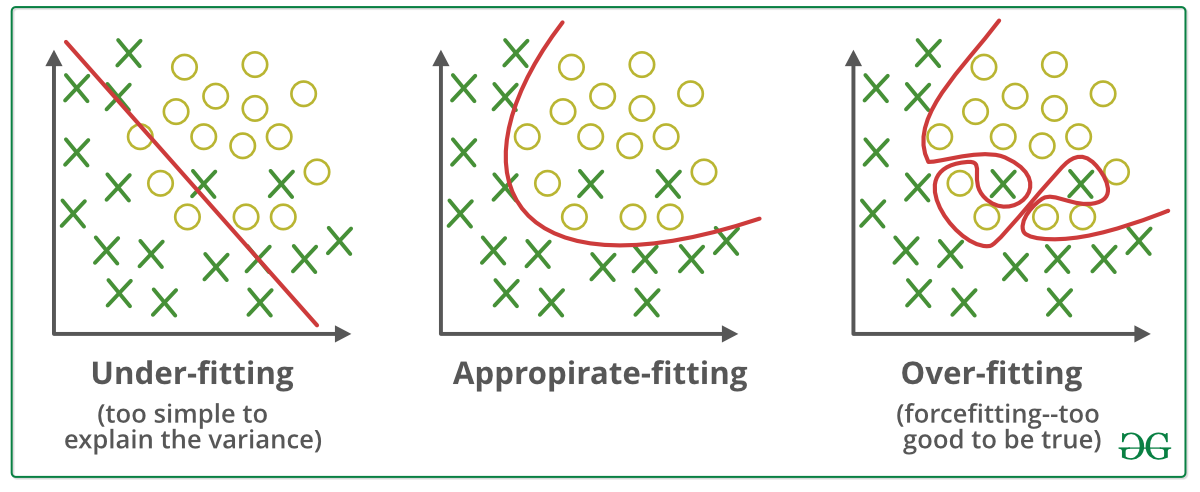
Niedopasowanie (ang. underfitting) - niezdolność hipotezy do właściwego odwzorowania danych uczących.

Wariancja - zmienność wyniku funkcji, wynikająca z (niewielkich) zmian w danych.

Przeuczenie lub nadmierne dopasowanie (ang. overfitting) - zbyt dokładne dopasowanie hipotezy do zbioru uczącego.

Kompromis między obciążeniem a wariancją (ang. bias-variance tradeoff) - wybór pomiędzy bardziej złożoną hipotezą, która dobrze dopasowuje się do danych, a prostszą hipotezą, która może lepiej się generalizować.

Generalizacja - zdolność modelu do generowania poprawnych wartości funkcji, na danych spoza dystrybucji danych uczących.

Niedopasowanie i nadmierne dopasowanie

 

 

Brzytwa Ockhama

 

 

Ockham's razor shaving Plato's beard - Stable Diffusion.

Wielość nie powinna być proponowana bez silnego uzasadnienia. Brzytwa została "użyta" do zgolenia "brody Platona".

Przykład - czekanie w restauracji

 

 

S. Russel, P. Norvig, AIMA 4rd edition.

Rzeczywiste drzewo decyzyjne - funkcja $f(x)$

 

 

S. Russel, P. Norvig, AIMA 4rd edition.

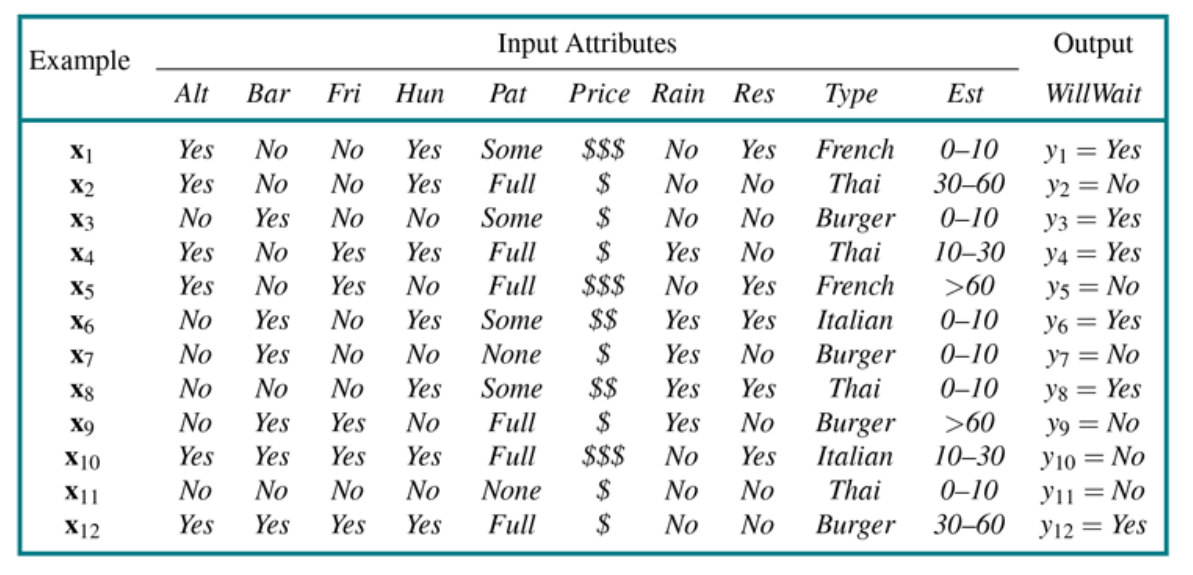
Jak powinniśmy wybierać atrybuty, żeby drzewo było najmniejsze?

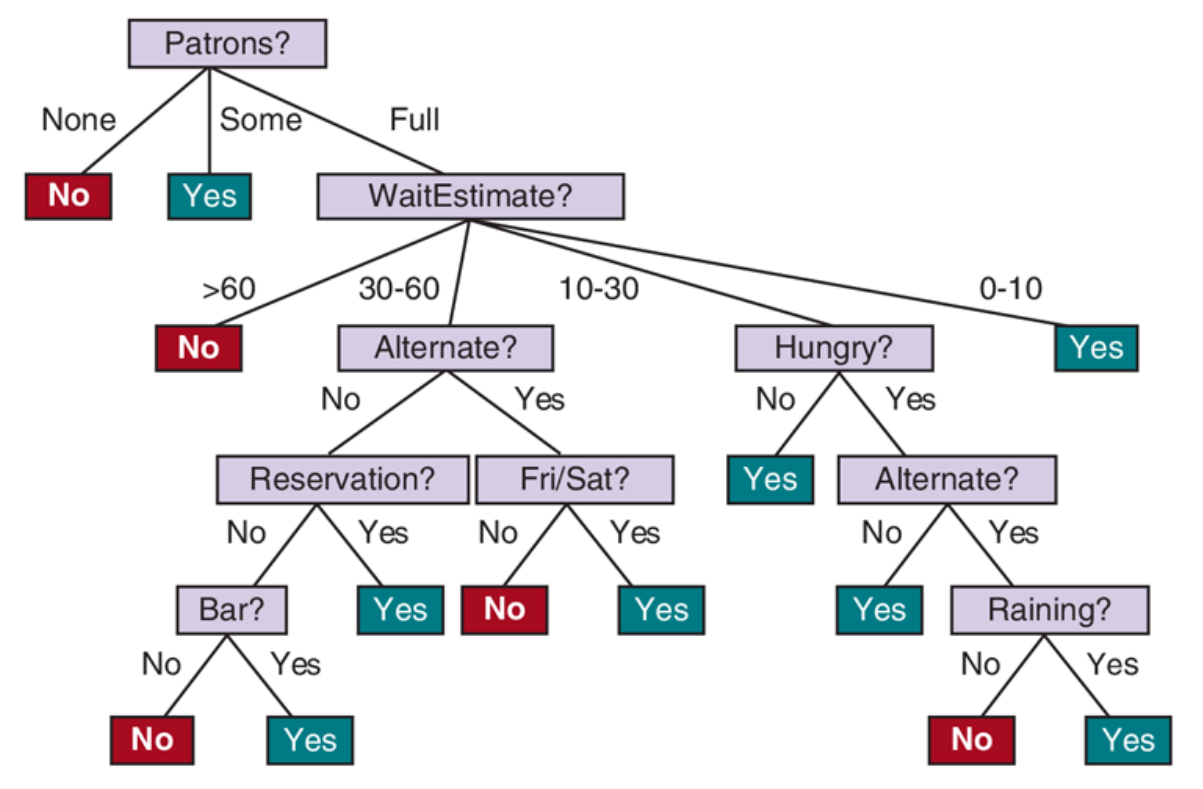
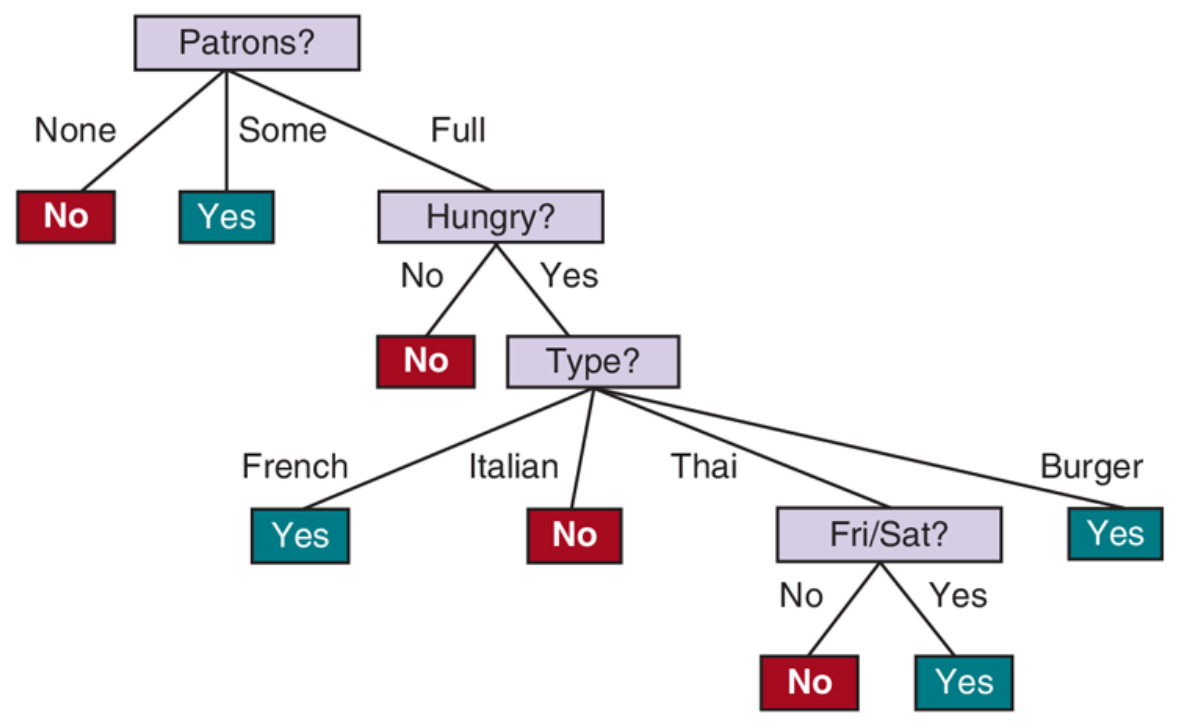
Indukcja drzewa decyzyjnego - hipotezy $\hat h_1(x)$ i $\hat h_2(x)$

 

 

S. Russel, P. Norvig, AIMA 4rd edition.

Indukcja drzewa decyzyjnego - algorytm uczenia

 

 

S. Russel, P. Norvig, AIMA 4rd edition.

Indukcja drzewa decyzyjnego - końcowe drzewo $\hat h(x)$

 

 

S. Russel, P. Norvig, AIMA 4rd edition.

Rozmiaru zbioru uczącego

 

 

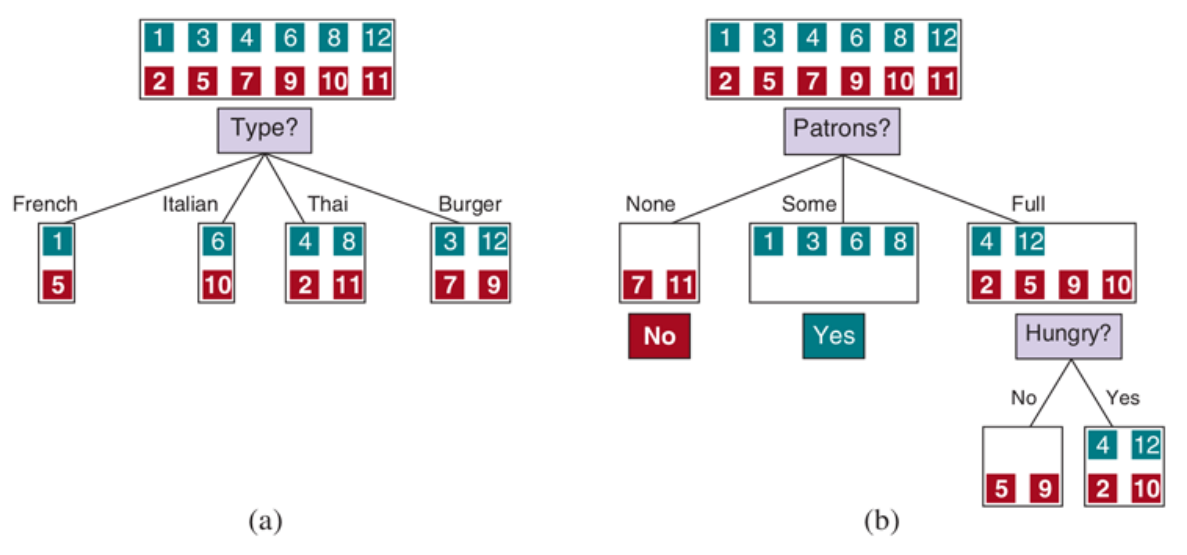
S. Russel, P. Norvig, AIMA 4rd edition.

Entropia i przyrost informacji

Entropia - miara niepewności na temat zmiennej losowej. Entropia jest tym mniejsza im więcej wiemy na temat zmiennej losowej.

$$ H(V) = \sum_k P(v_k)\log_2 \frac{1}{P(v_k)} = - \sum_k P(v_k)\log_2 P(v_k) $$

• $H$ - entropia
• $V$ - zmienna losowa
• $v_k$ - wartości zmiennej losowej
• $P(v_k)$ - prawdopodobieństwo wartości $v_k$

$$ B(q) = -((q \log_2 q) + (1 - q)\log_2(1-q)) $$

• $B$ - entropia binarnej zmiennej losowej
• $q$ - prawdopodobieństwo klasy pozytywnej

$$ H(Output) = B\left(\frac{p}{p+n}\right) $$

• $p$ - liczba przykładów pozytywnych
• $n$ - liczba przykładów negatywnych

$$ Remainder(A) = \sum_{k=1}^{d} \frac{p_k + n_k}{p + n}B\left(\frac{p_k}{p_k + n_k}\right) $$

• $A$ - wybrany atrybut drzewa decyzyjnego
• $d$ - liczba wartości atrybutu $A$
• $E_1$ - $E_d$ - podzbiory przykładów pozostające po wybraniu atrybutu $A$

Jest to wartość oczekiwana entropi po wyborze atrybutu A.

$$ Gain(A) = B\left(\frac{p}{p+n}\right) - Remainder(A) $$

 

 

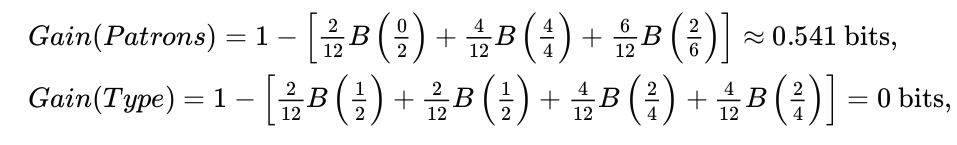
S. Russel, P. Norvig, AIMA 4rd edition.

Ocena modeli uczenia maszynowego

https://www.studying-in-uk.org/information-on-predicted-grades-for-independent-applicants-in-the-uk/

Macierz pomyłek

 

 

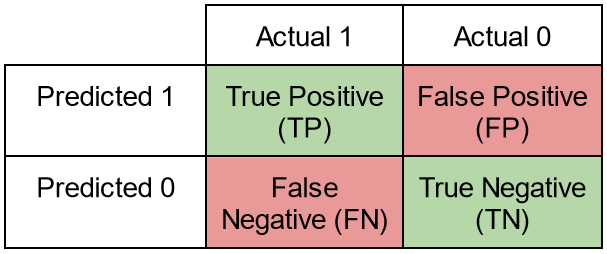
Przypadki

• prawdziwie pozytywne (true positive TP) - model zwrócił klasę pozytywną (positive), i jest to prawda (true)
• prawdziwie negatwyne (true negative TN) - model zwrócił klasę negatywną (negative), i jest to prawda (true)
• fałszywie negatywne (false negative FN) - model zwrócił klasę negatywną (negative), ale nie jest to prawda (false)
• fałszywie pozytywne (false positive FP) - model zwrócił klasę pozytywną (positive), ale nie jest to prawda (false)

Dokładność (celność, accuracy)

$$ Acc = \frac{TP + TN}{TP + TN + FP + FN} $$

Dlaczego nie wystarcza nam dokładność?

Zbiór zbalansowany i niezbalansowany

Precyzja, miara predykcyjna dodatnia (precision)

$$ Pr = \frac{TP}{TP + FP} $$

Czułość, pokrycie (recall)

$$ Rc = \frac{TP}{TP + FN} $$

Miara $F_1$

$$ F_1 = \frac{2 Pr Rc}{Pr + Rc} $$

Miara $F_\beta$

$$ F_{\beta} = (1 + \beta^2)\frac{PrRc}{(\beta^2 Pr) + Rc} $$

 

  https://en.wikipedia.org/wiki/F-score

AUROC

 

  https://glassboxmedicine.com/2019/02/23/measuring-performance-auc-auroc/

 

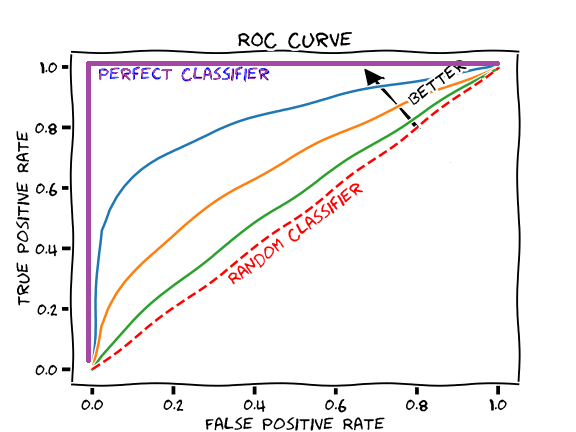
  https://www.researchgate.net/publication/338909223_Artificial_Intelligence_Technique_for_Gene_Expression_by_Tumor_RNA-Seq_Data_A_Novel_Optimized_Deep_Learning_Approach/figures

Funkcja kosztu (ang. loss, również funkcja celu)

Błąd średniokwadratowy (mean squared error - MSE):

$$ C(X) = \frac{1}{N}\sum_{i=1}^{N}(y_i - \hat y_i)^2 = \frac{1}{N} || y - \hat y ||_2^2 $$

Błąd bezwzględny (mean absolute error - MAE):

$$ C(X) = \frac{1}{N}\sum_{i=1}^N | y_i - \hat y_i| = \frac{1}{N}|| y - \hat y||_1 $$

Błąd binarny:

$$ C(X) = \frac{1}{N} \sum_{i=1}^N 1 - \delta(y_i, \hat y_i) $$

Symbol/delta Kroneckera

Entropia skrośna:

$$ H(p,q) = - \sum_{x \in X} p(x) \log q(x) $$

$$ C(X)= - \frac{1}{N} \sum_{i=1}^N \left(y_i \log \hat y_i + (1 - y_i)\log(1 - \hat y_i)\right) $$

W zależności od funkcji celu będziemy otrzymywali różne wyniki. Opracowanie właściwej funkcji celu jest jednym z istotniejszych zadań dla określonego problemu badawczego.

Przedstawione funkcje mają zastosowanie np. w odniesieniu do regresji liniowej. W przypadku danych dyskretnych używamy innych funkcji kosztu.

 

 

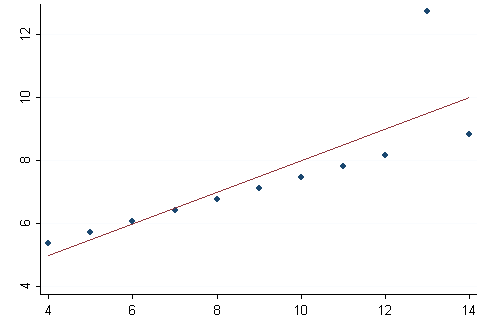
Regularyzacja $L_2$ z błędem kwadratowym jako funkcją kosztu

$$ C(X) = \sum_{i=1}^N (y_i - \hat y_i)^2 + \lambda \sum_{j=1}^M w_j^2 = ||y - \hat y||_2^2 + \lambda ||w||_2^2 $$

• $\lambda$ - hiperparametr, który będzie decydował na ile istotne są dane treningowe, a na ile regularyzacja

Regularyzacja $L_1$ z błędem kwadratowym jako funkcją kosztu

$$ C(X) = \sum_{i=1}^N (y_i - \hat y_i)^2 + \lambda \sum_{j=1}^M |w_j| = ||y - \hat y||_2^2 + \lambda ||w||_1 $$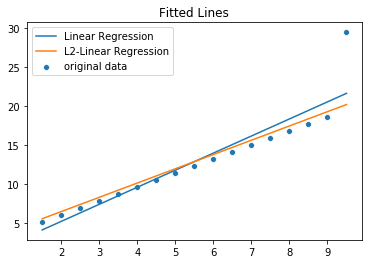

Koszt generalizacji oraz koszt empiryczny

$$ GenLoss_L(h) = \sum_{(x,y) \in \epsilon} L(y, h(x))P(x,y) $$

• $\epsilon$ - zbiór wszystkich możliwych par

• $P(x,y)$ - rozkład prawdopodobieństwa par (x, y).

$$ h^* = \textrm{arg}\min_{h \in H} GenLoss_L(h) $$

$$ EmpLoss_L(h) = \sum_{(x,y) \in \epsilon} L(y, h(x))\frac{1}{N} $$

Koszt generalizacji jest tym, którego poszukujemy, tzn. chcemy znaleźć funkcję, która dla rzeczywistego rozkładu danych daje najelpsze wyniki.

Ale w rzeczywistości nie mamy dostępu do $P(x,y)$. Ponadto zbiór testowy jest znacznie mniejszy. Dlatego najczęściej korzystamy z kosztu empirycznego.

Dlaczego istotne jest aby rozkład w próbce odzwierciedlał rozkład rzeczywisty?

 

 

https://www.alamy.com/stock-photo-an-aerial-view-showing-tanks-and-infantry-of-the-american-6th-armored-105370917.html

Jest to jeden z najpoważniejszych problemów w treningu dobrego modelu uczenia maszynowego. Mogą wystąpić następujące problemy:

• możemy "wylosować" dane, które będą posiadały cechy charakterystyczne, ułatwiające klasyfikatorowi podjęcie decyzji, które to dane nie będą występować w rzeczywistości (zdjęcia z chmurami i czołgami)
• możemy "wylosować" dane, które nie odzwierciedlają rzeczywistego rozkładu, są jego zaprzeczeniem, wtedy model będzie a priori dawał odwrotne P dla klas, niż mają one w rzeczywistości.

Dlatego tak ważne jest pozyskanie rzeczywistych danych, do uczenia modeli.

Przyczyny rozbieżności między $\hat h(x)$ a $f(x)$

• realizowalność - przestrzeń $H$ nie zawiera $f$

• wariancja - jeśli funkcja jest realizowalna, to ze wzrosem liczby przykładów wariancja będzie spadać

• szum (brak determinizmu) - funkcja zwraca różne wartości dla tych samych danych wejściowych

• złożoność obliczeniowa - problemem jest odnalezienie właściwej hipotezy w przestrzeni $H$

Parametry i hiperparametry modelu

 

 

https://wandb.ai/site/articles/fundamentals-of-neural-networks

Hiperparametry

 

 

https://www.akira.ai/glossary/hyperparameter-tuning

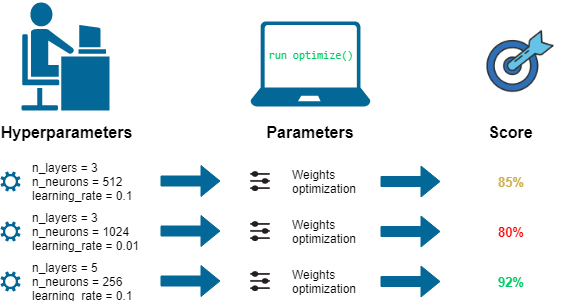
Przykładowe hiperparametry

• maksymalna głębokość drzewa decyzyjnego
• liczba (rozmiar podzbioru) atrybutów w lasie decyzyjnym
• stała ucząca w algorytmie spadku wzdłuż gradientu
• liczba epok uczących
• siła parametru regularyzującego (stała $\lambda$)
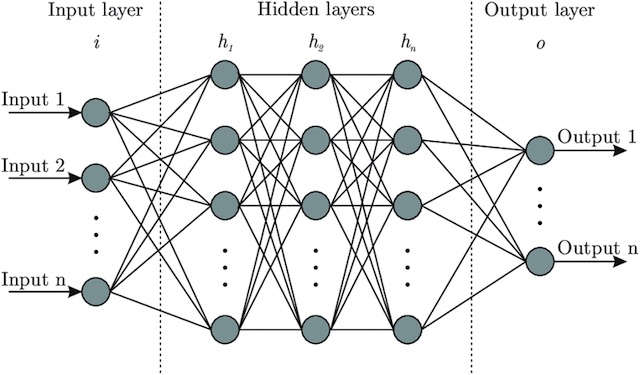
• architektura sieci neuronowej
• ...

Zbiór treningowy, testowy i walidacyjny

 

 

https://sdsclub.com/how-to-train-and-test-data-like-a-pro/

Funkcja kosztu

 

 

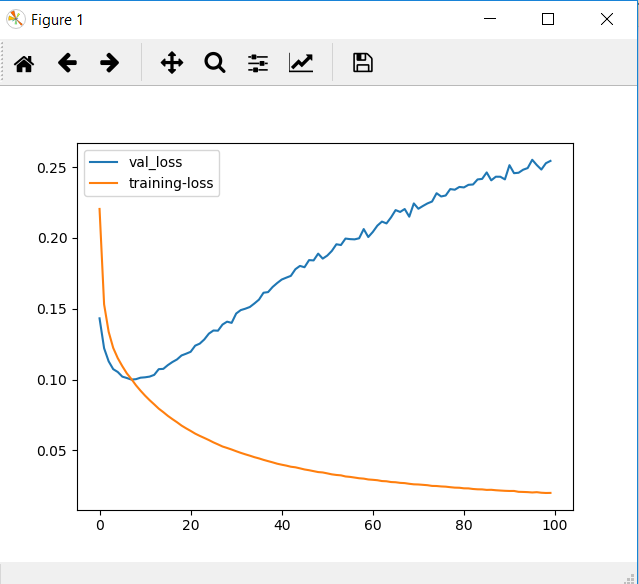
https://datascience.stackexchange.com/questions/53645/regarding-training-loss-and-validation-loss

Walidacja krzyżowa

 

 

</small>

Załóżmy, że tworzmy model odpowiadający na pytania prawne. Mamy pytania dotyczące 3 ustaw: konstytucji (60%), kodeksu cywilnego (35%) i kodeksu karnego (5%). Jak utworzymy zbiór treningowy, a jak testowy?