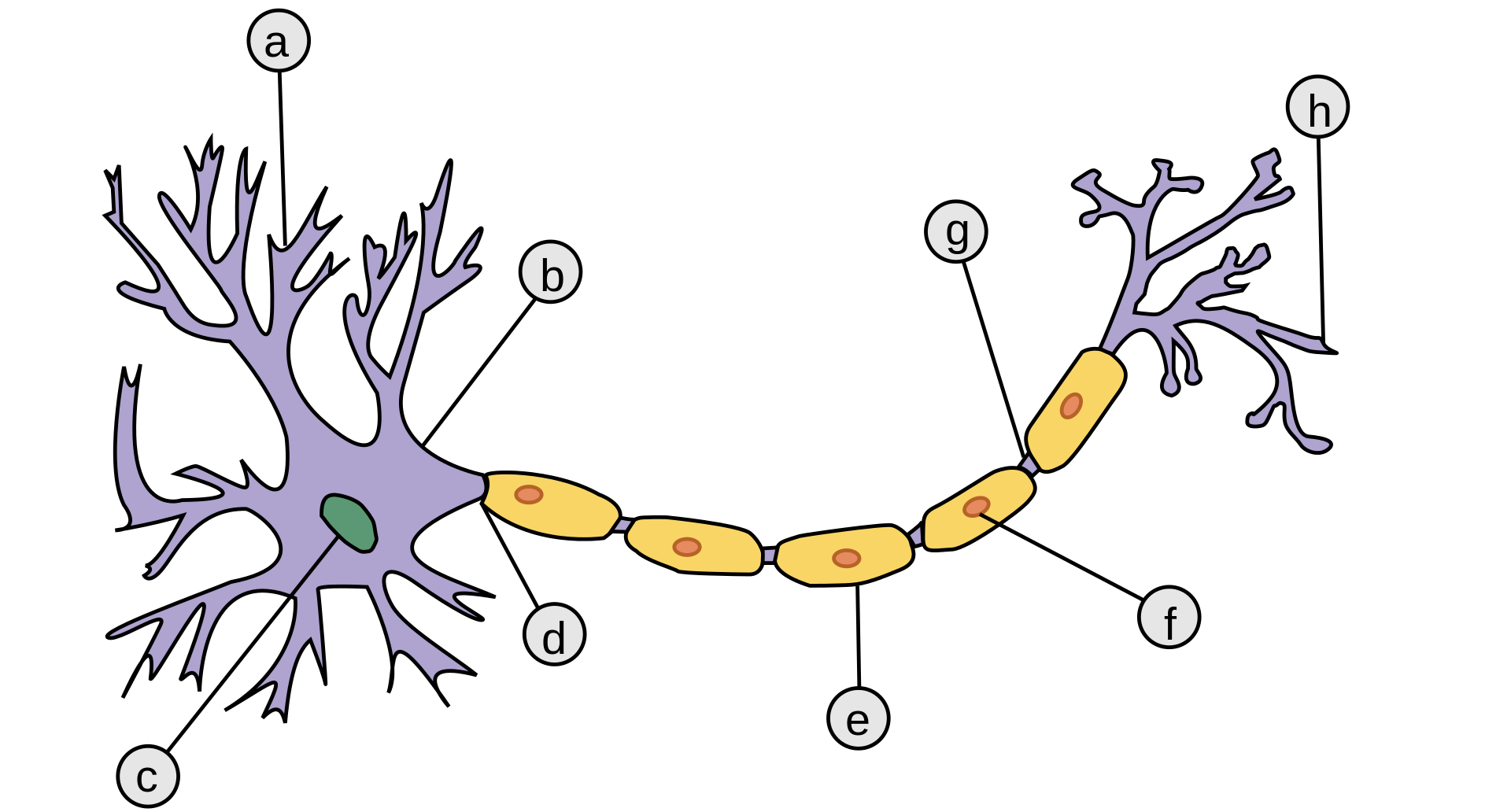
Naturalne i sztuczne sieci neuronowe¶
 |
 |
 |
 |
Wielkość sieci neuronowej¶
- Liczba neuronów w mózgu: $1,5-1,6 * 10^{11}$ (setki miliardów)
- Liczba połączeń w mózgu: $10^{14}$ (setki bilionów)
- Liczba parametrów w sieci neuronowej: $1,75 * 10^{12}$ (biliony parametrów, model WuDao)
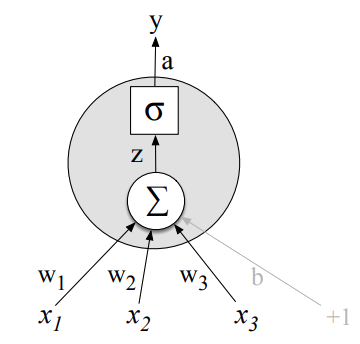
sumowanie sygnałów od porzedzających neuronów
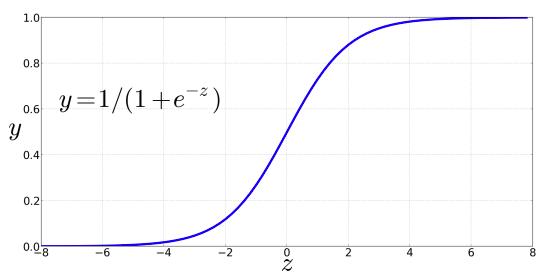
$$ z = w_1 x_1 + \cdots + w_i x_i + \cdots w_k x_k + b $$$$ z = \boldsymbol{w} \cdot \boldsymbol{x} + b $$Sigmoida
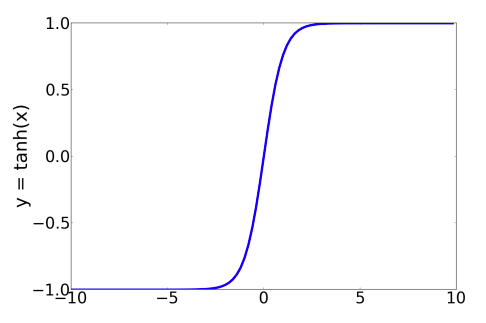
$$ \sigma(z) = \frac{1}{1 + e^{-z}} $$Tangens hiperboliczny
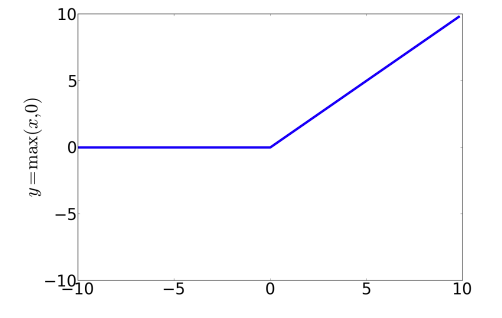
$$ \tanh(z) = \frac{e^z - e^{-z}}{e^z+e^{-z}} $$Rektyfikowana jednostka liniowa
(rectified linear unit)
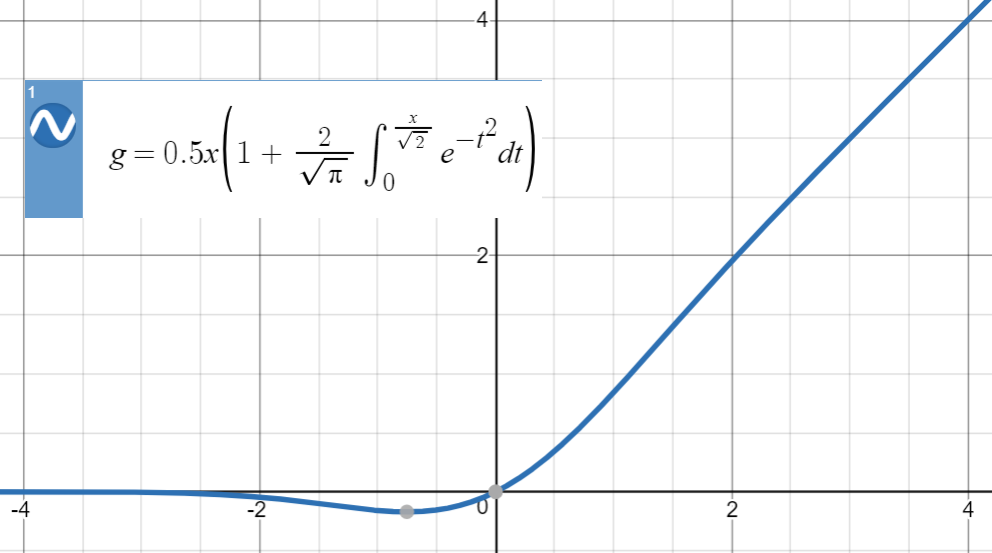
Jednostka liniowa z błędem gaussowskim
Gaussian error linear unit
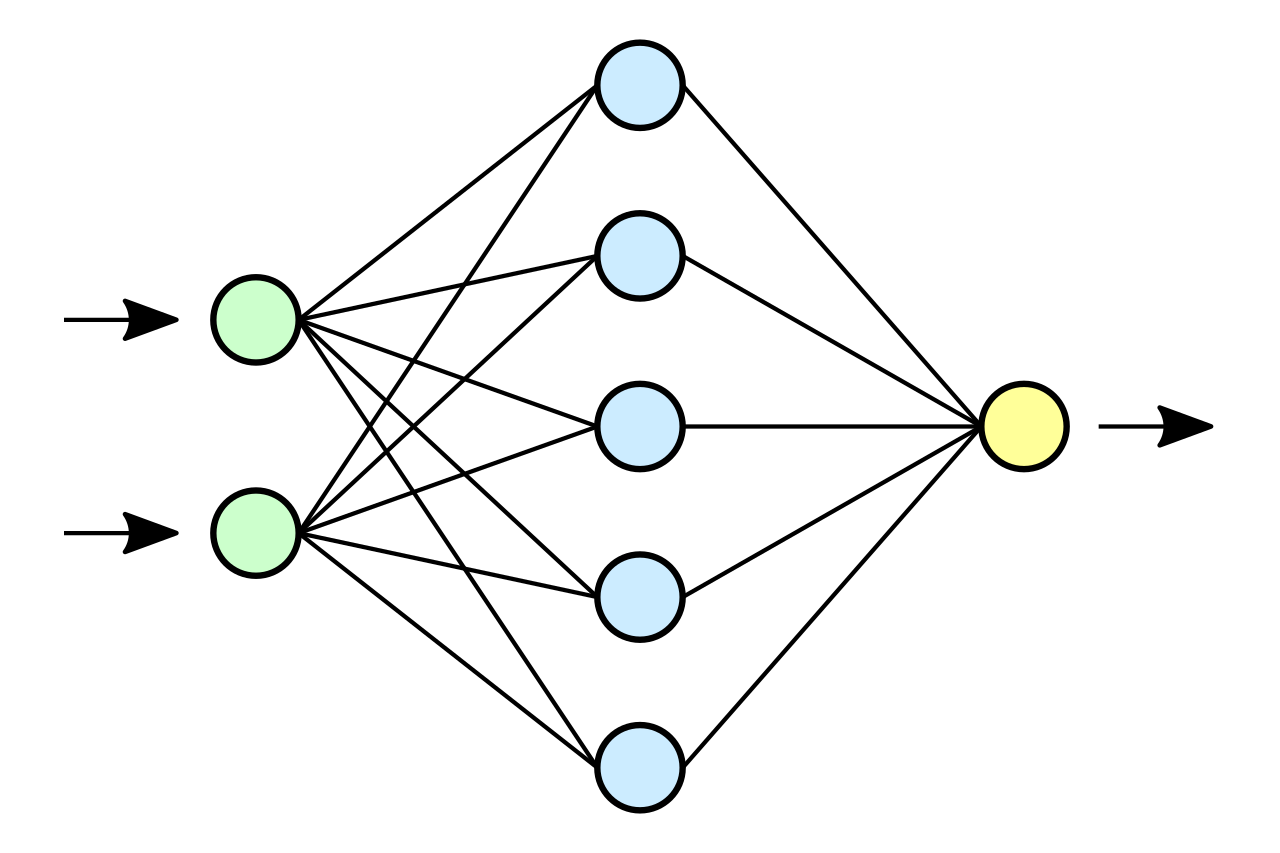
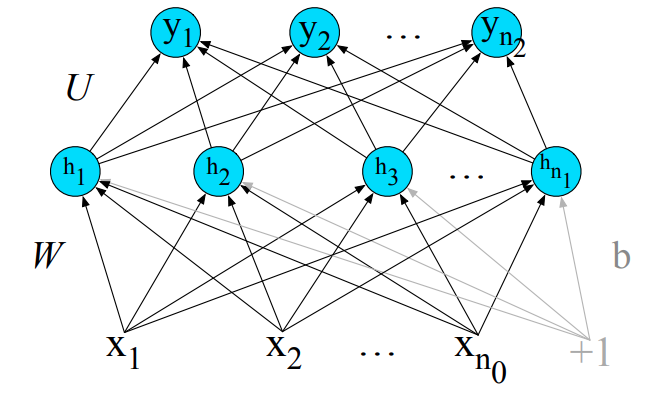
Typowa sieć neuronowa składa się z:
- warstwy wejściowej (kolor zielony), która akceptuje wektor danych wejściowych
- warstw/y ukrytej/ych (kolor niebieski - jedna lub wiele warstw),
- warstwy wyjściowej (kolor żółty), która generuje odpowiedź sieci.
Uniwersalny aproksymator
Sieć neuronowa z nieliniową funkcją aktywacji stanowi uniwersalny aproksymator, tzn. może aproksymować dowolną funkcję:
$$ f(x): \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} $$Reprezentacja danych wejściowych¶
- dane tabelaryczne: $\mathbb{R}^n$, nieuporządkowane wartości dyskretne kodowane jako wektory 1-hot-encoding
- dane sekwencyjne:
- pojedynczy punkt danych reprezentowana jako wektor $\mathbb{R}^n$, aktywacja sieci jest zachowywana dla kolejnego punktu,
- sekwencja punktów danych o maksymalnej długości $k$, uzupełniona o wektory dłuości $m$ kodujące pozycję: $\mathbb{R}^{(n+m) \times k}$
- dane tekstowy:
- reprezentowane jak dane sekwencyjne, wyrazy nie są kodowane jako 1-hot-encoding, ale jako osadzenia (embeddings)
Wartość funkcji¶
- pojedynczy neuron $\mathbb{R}$ - regresja
- dwa neurony, dla których stosowana jest funkcja softmax
$\sigma(\boldsymbol{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{2} e^{z_j}}$ - klasyfikacja binarna.
- K neuronów, dla których stosowana jest funkcja soft-max - klasyfikacja wieloklasowa
- wartościami mogą być również tensory wielowymiarowe
Funkcja straty¶
Entropia krzyżowa:
$$ H(P,Q) = \boldsymbol{E}_{\boldsymbol{z} \sim P(\boldsymbol{z})}\left[\log Q(\boldsymbol{z})\right] = \int P(\boldsymbol{z})\log Q(\boldsymbol{z}) d\boldsymbol{z} $$Pytanie: dlaczego potrzebne jest kodowanie pozycji dla sekwencyjnych danych wejściowych przetwarzanych przez sieć w pełni połączoną?¶
Sieć konwolucyjna¶
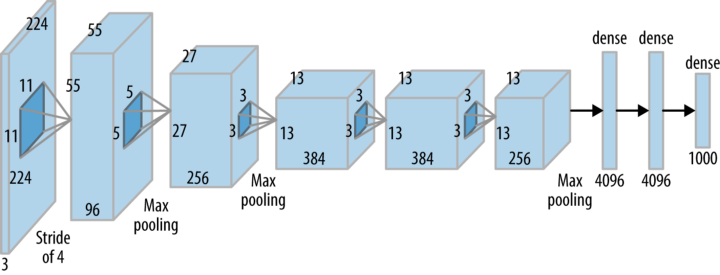
Filtry sieci konwolucyjnej¶

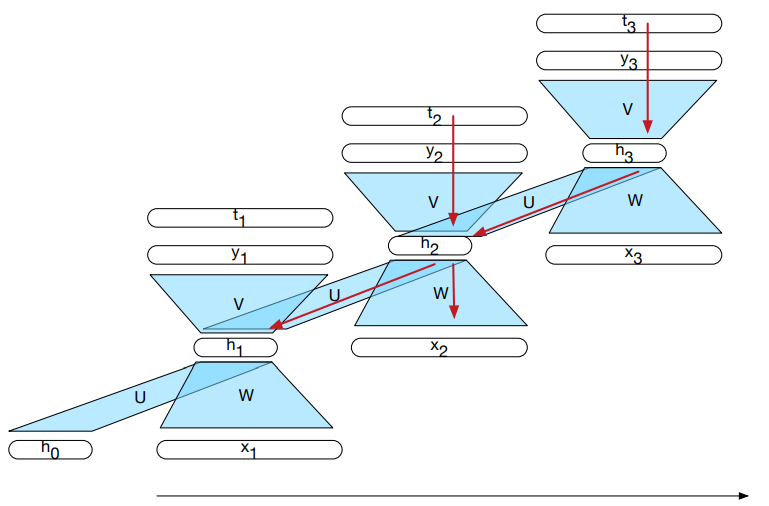
Sieć rekurencyjna¶
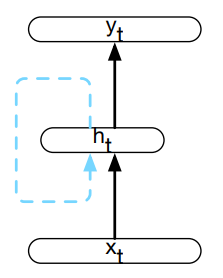
Sieć rekurencyjna (rozwinięcie)¶
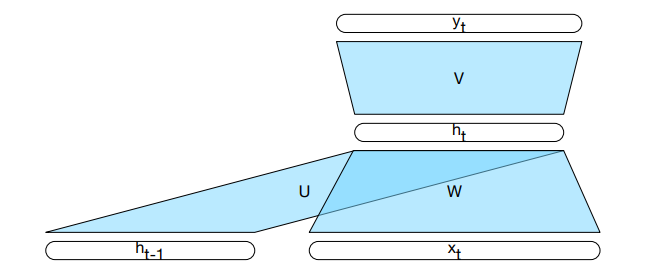
Sieć transformacyjna¶
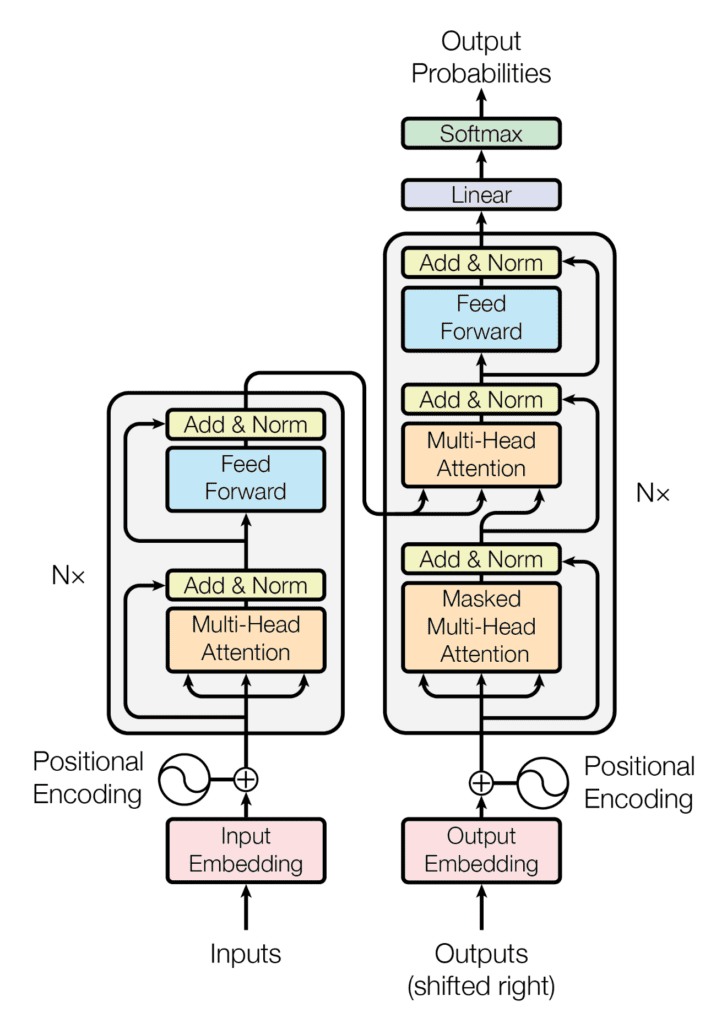
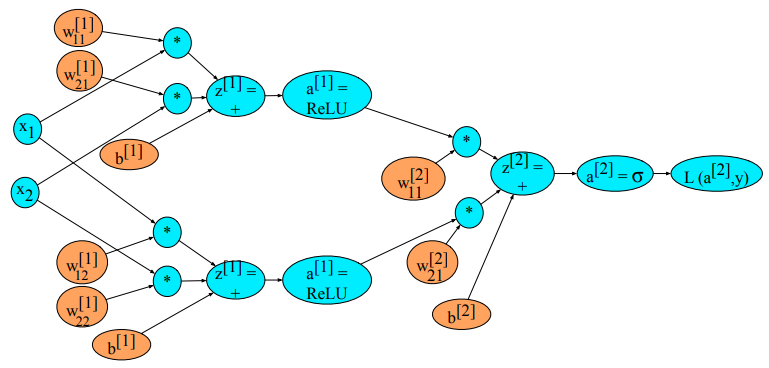
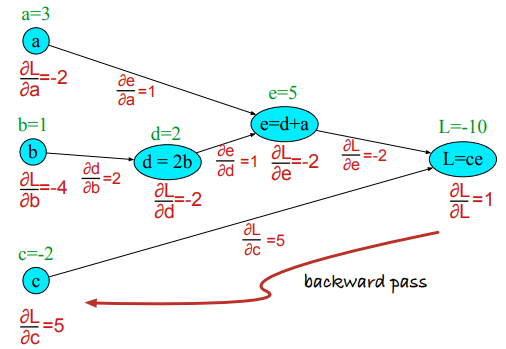
Reguła łańcuchowa¶
$$ \frac{\partial g(f(x))}{\partial x} = g'(f(x))\frac{\partial f(x)}{\partial x} $$$$ \frac{dg}{dx} = \frac{dg}{df}\cdot\frac{df}{dx} $$
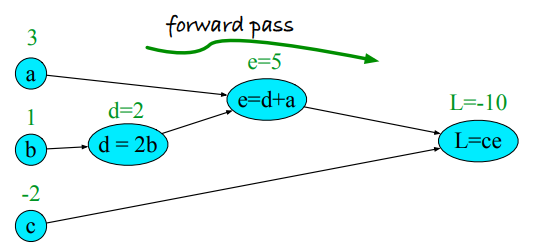

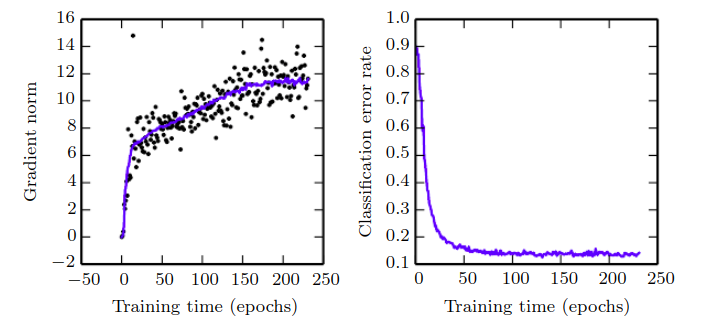
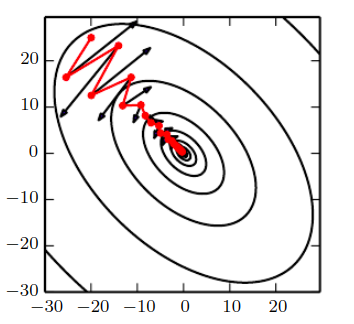
Pomimo tego, że wartość funkcji straty maleje, to norma z gradientu rośnie. Oznacza to, że proces nie osiąga minimum.
Lokalne minima¶
- optymalny model nie jest identyfikowalny
- model identyfikowlany, to model, który przy odpowiedniej liczbie danych uczących eliminuje wszystkie pozostałe modele, tzn. istnieje tylko jeden optymalny model
- symetria przestrzeni wag - możliwe jest zamienienie ze sobą wag połączeń wchodzących i wychodzących dla pary neuronów w obrębie jednej warstwy, bez wpływu na wartość funkcji straty
- skalowanie wag - przeskalowanie wagi połączenia wchodzącego przez $\alpha$ oraz wychodzącego przez $1/\alpha$ dla rektyfikowanej jednostki liniowej również nie wpływa na wartość funkcji straty
- wszystkie takie minima są ekwiwalentne względem siebie
- weryfikacja czy mamy do czynienia z minimum loklanym opiera się na wyświetleniu wartości normy gradientu - jeśli nie spada, to nie mamy do czynienia z minimum lokalnym
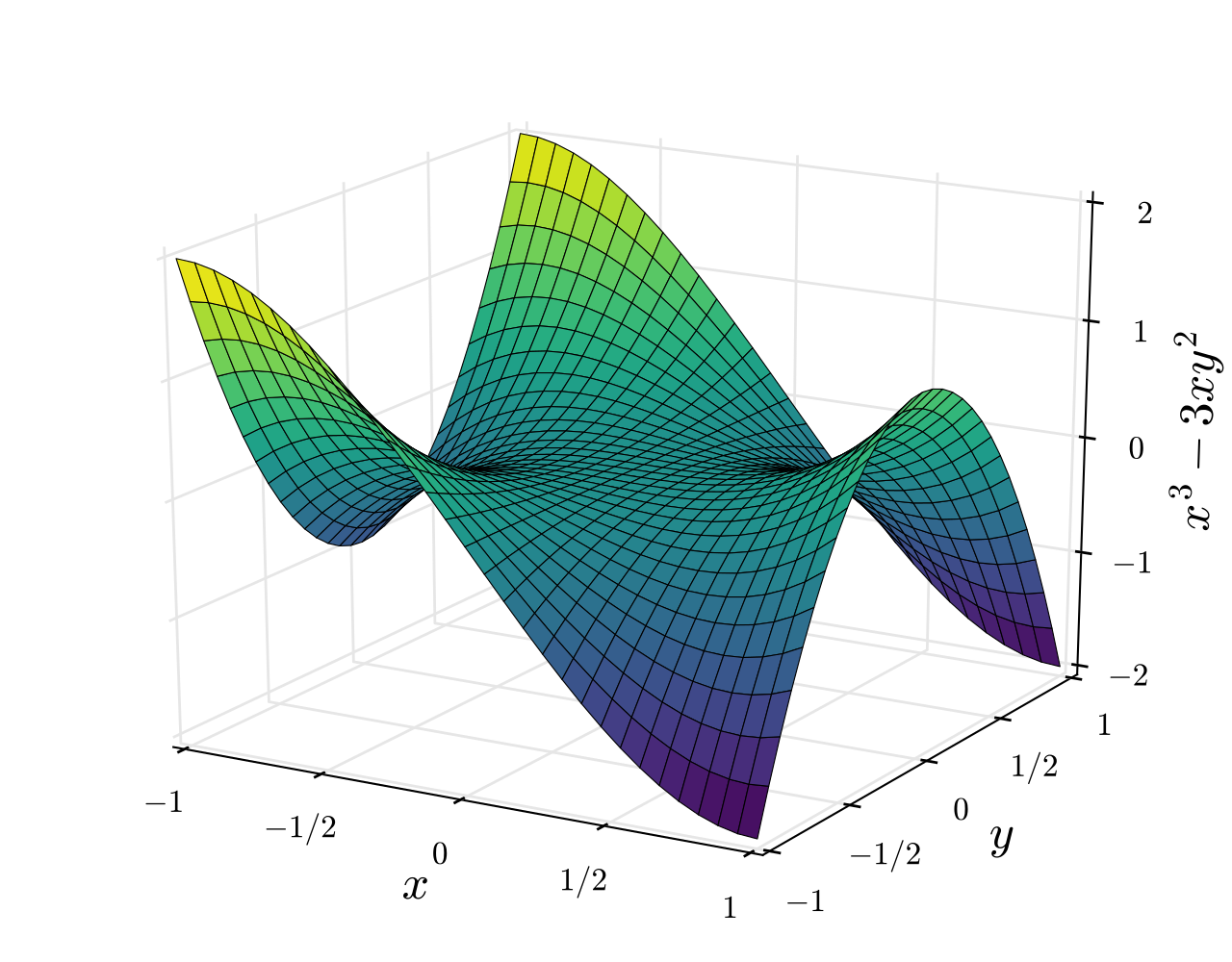
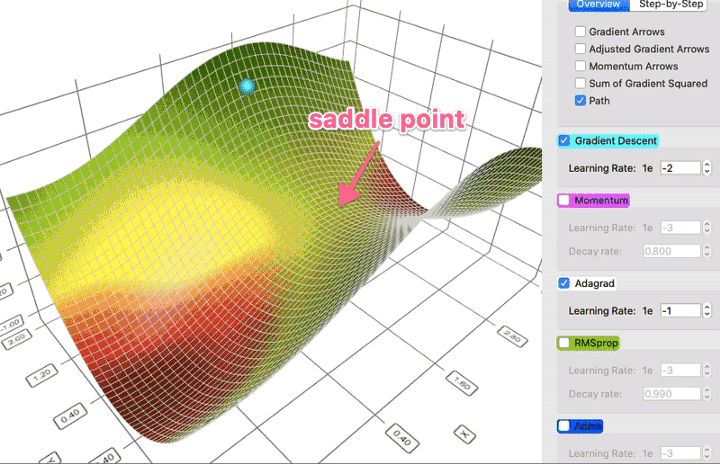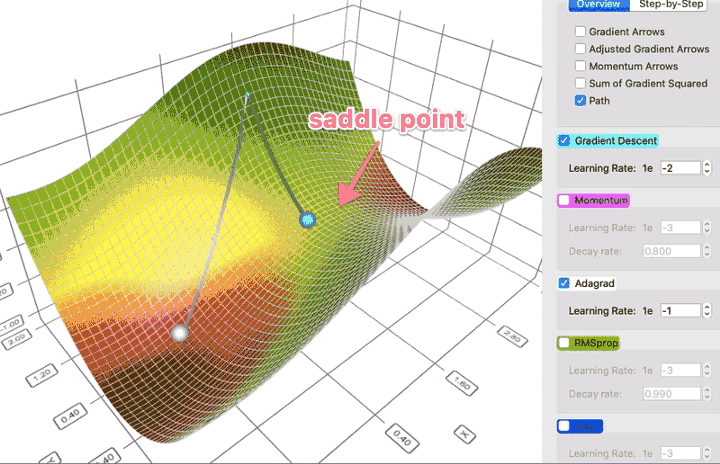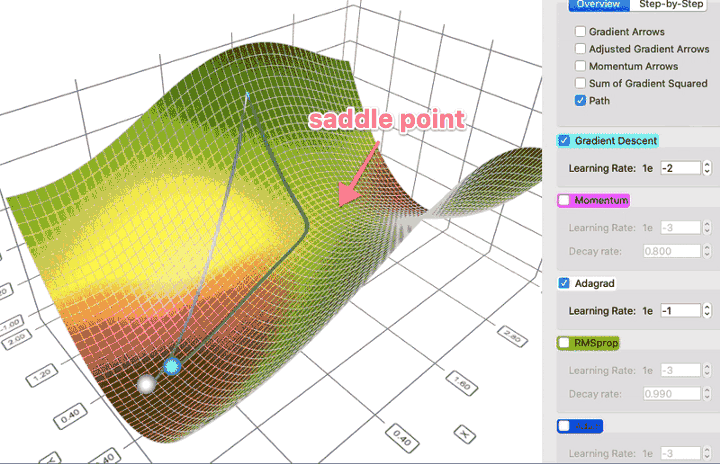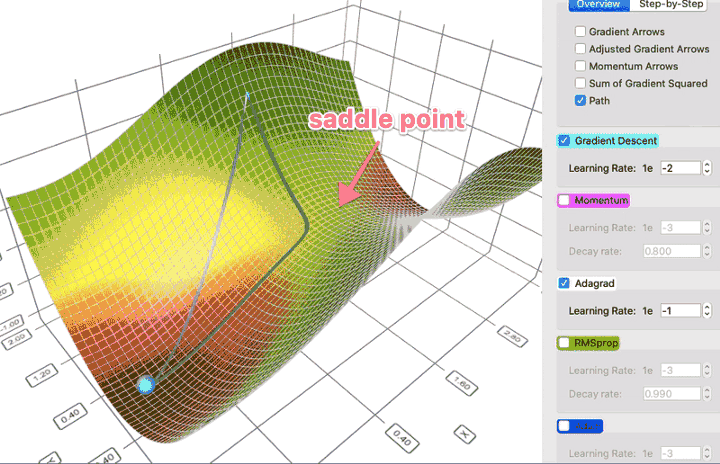
- liczba punktów siodłowych dla funkcji wielowymiarowej jest większa niż liczba lokalnych minimów
- przyczyną jest fakt, że wystąpienie miminum lokalnego występuje gdy hesjan macierzy jest dodatnio-określony
- w przypadku punktu sidołowego, część wartości własnych hesjana jest dodatnia, a część ujemna
- uzyskanie mimimum lokalnego jest znacznie mniej prawdopodobne, bo wymaga by wszystkie wartości własne były dodatnie - zakładając, że wartości te są losowane, prawdopodobieństwo jest eksponencjalnie mniejsze, w zależności od liczby wymiarów
- w okolicy punktu siodłowego gradient może być bardzo mały, co wygląda jak wpadnięcie do minimum lokalnego
Eksplodujący gradient¶
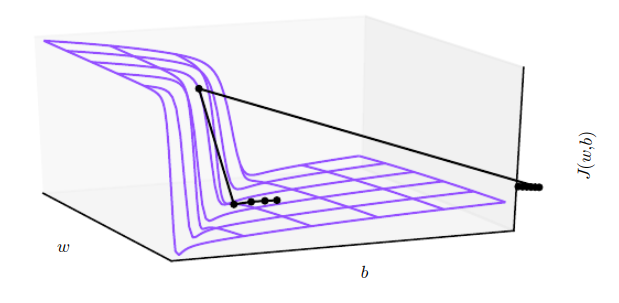
- klify powstają w sytuacji mnożenia kilkiu wag o wysokiej wartości, co ma miejsce w przypadku sieci rekurencyjnych
- ograniczanie gradientu (gradient clipping) pozwala zmniejszyć ryzyko "spadku z klifu"
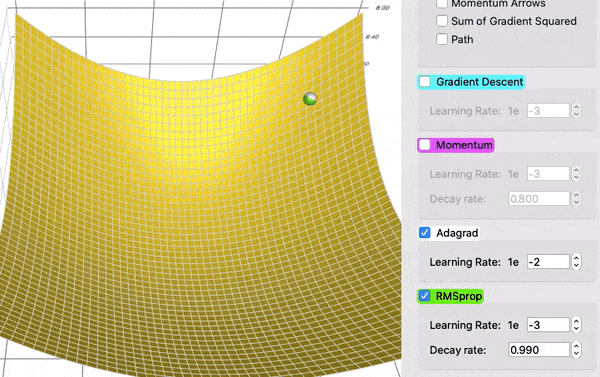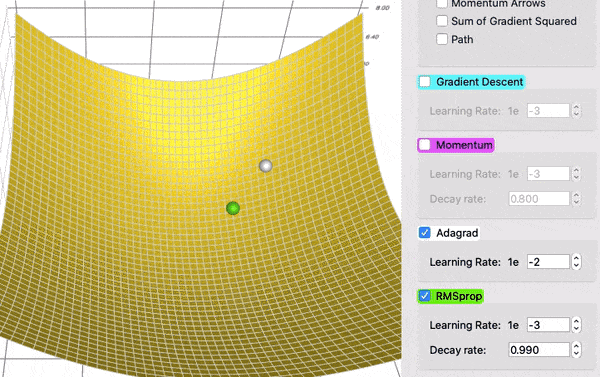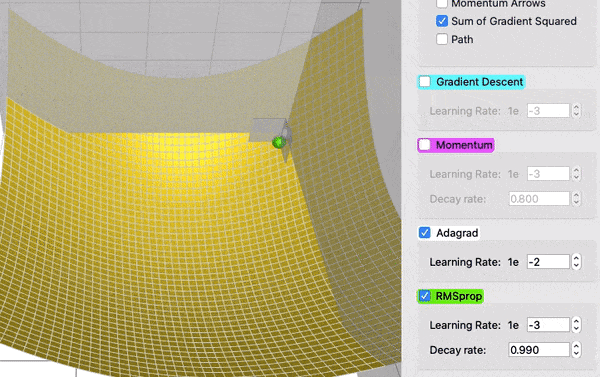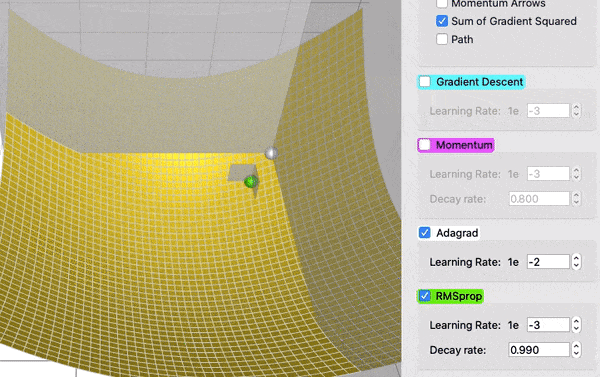
Optymalizacja parametrów¶
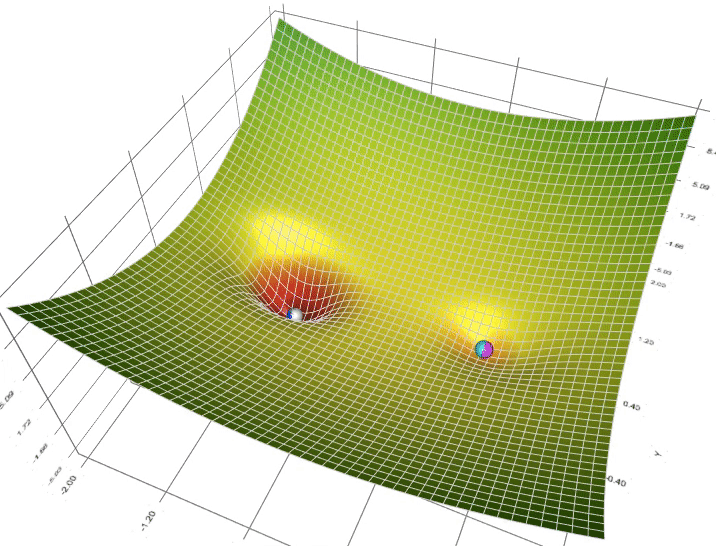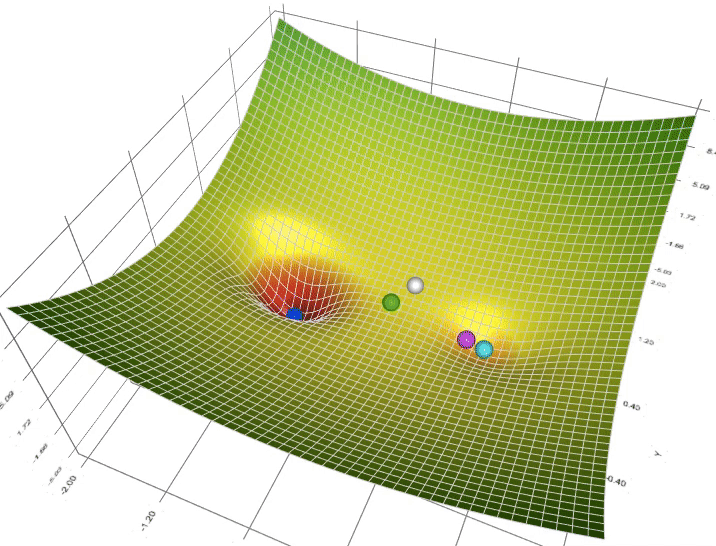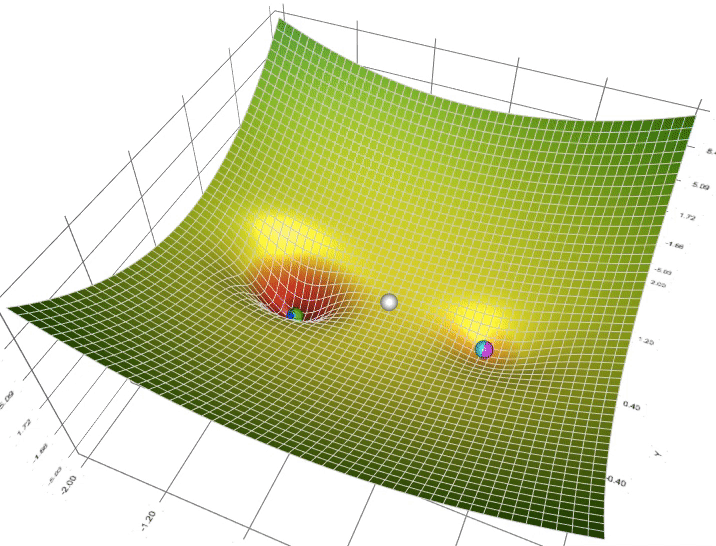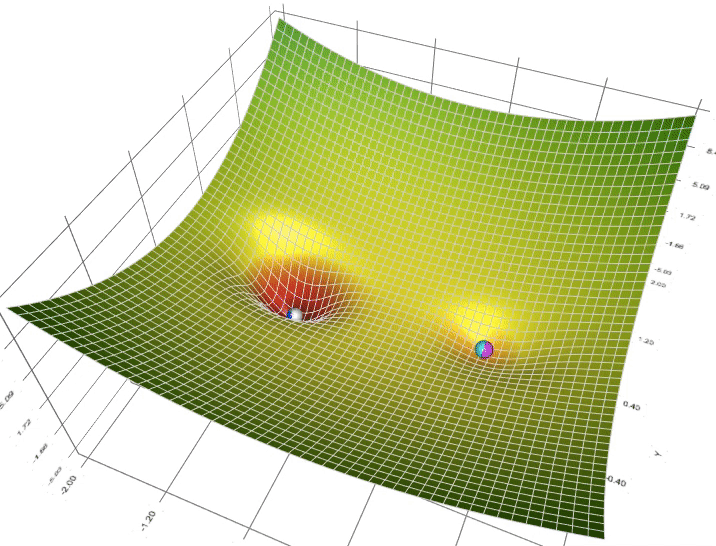
https://towardsdatascience.com/a-visual-explanation-of-gradient-descent-methods-momentum-adagrad-rmsprop-adam-f898b102325c
(Stochastic) Gradient Descent (SGD)¶
$$ \boldsymbol{w^*} = arg\min_{\boldsymbol{w}} \left(- \sum_{j=1}^m \log P_{\boldsymbol{w}}(\boldsymbol{y}_j|\boldsymbol{x}_j)\right) $$- N - rozmiar zbioru treningowego
- m = N $\rightarrow$ graident descent
- m = 1 $\rightarrow$ stochastic gradient descent
- m > 1 i m < N $\rightarrow$ (minibatch) stochastic gradient descent
SGD¶
- Istotne jest aby przykłady należące do m były wybrane w sposób losow (dlaczego?)
- W praktyce wystarczy jednokrotnie zmienić kolejność elementów w całym zbiorze, a następnie wybierać kolejne paczki z tak zmodyfikowanego zbioru.
- W optymalnym scenariuszu w trakcie procesu uczenia model wykorzystuje określony przykład uczący tylko raz (1 epoka uczenia)
- W praktyce zbiory uczące są zbyt małe (z wyjątkiem sytuacji określanych jako self-supervised learning), aby można było wykonać tylko jedną epokę
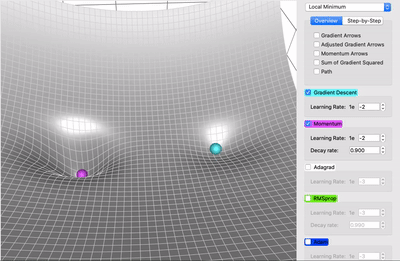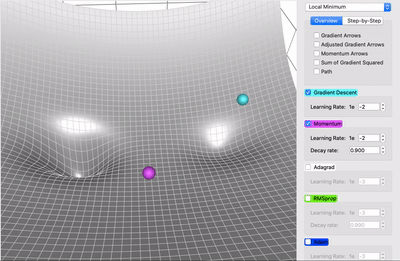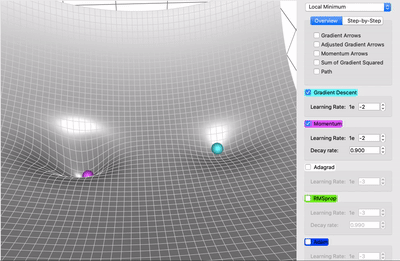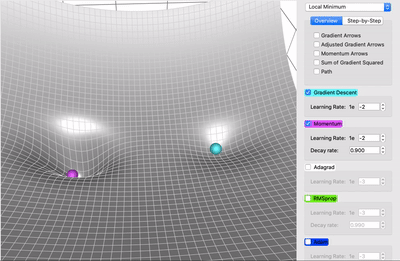
https://towardsdatascience.com/a-visual-explanation-of-gradient-descent-methods-momentum-adagrad-rmsprop-adam-f898b102325c
from IPython.lib.display import YouTubeVideo
YouTubeVideo('ilYd4TAzNoU', 1120, 630)